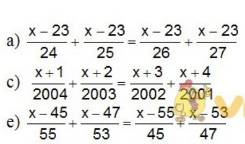\(a,\\ \dfrac{x-23}{24}+\dfrac{x-23}{25}=\dfrac{x-23}{26}+\dfrac{x-23}{27}\\ \Leftrightarrow\dfrac{x-23}{24}+\dfrac{x-23}{25}-\dfrac{x-23}{26}-\dfrac{x-23}{27}=0\\ \Leftrightarrow\left(x-23\right)\left(\dfrac{1}{24}+\dfrac{1}{25}-\dfrac{1}{26}-\dfrac{1}{27}\right)=0\)
mà `1/24+1/25-1/26-1/27 \ne 0`
nên `x-23=0`
`x=23`
\(c,\\ \dfrac{x+1}{2004}+\dfrac{x+2}{2003}=\dfrac{x+3}{2002}+\dfrac{x+4}{2001}\\ \Leftrightarrow\left(\dfrac{x+1}{2004}+1\right)+\left(\dfrac{x+2}{2003}+1\right)=\left(\dfrac{x+3}{2002}+1\right)+\left(\dfrac{x+4}{2001}+1\right)\\ \Leftrightarrow\dfrac{x+2005}{2004}+\dfrac{x+2005}{2003}=\dfrac{x+2005}{2002}+\dfrac{x+2005}{2001}\\ \Leftrightarrow\dfrac{x+2005}{2004}+\dfrac{x+2005}{2003}-\dfrac{x+2005}{2002}-\dfrac{x+2005}{2001}=0\\ \Leftrightarrow\left(x+2005\right)\left(\dfrac{1}{2004}+\dfrac{1}{2003}-\dfrac{1}{2002}-\dfrac{1}{2001}\right)=0\\ \Leftrightarrow x+2005=0\left(\dfrac{1}{2004}+\dfrac{1}{2003}-\dfrac{1}{2002}-\dfrac{1}{2001}\ne0\right)\\ \Rightarrow x=-2005\)
\(e,\\ \dfrac{x-45}{55}+\dfrac{x-47}{53}=\dfrac{x-55}{45}+\dfrac{x-53}{47}\\ \Leftrightarrow\left(\dfrac{x-45}{55}-1\right)+\left(\dfrac{x-47}{53}-1\right)-\left(\dfrac{x-55}{45}-1\right)-\left(\dfrac{x-53}{47}-1\right)=0\\ \Leftrightarrow\dfrac{x-100}{55}+\dfrac{x-100}{53}-\dfrac{x-100}{45}-\dfrac{x-100}{47}=0\\ \Leftrightarrow\left(x-100\right)\left(\dfrac{1}{55}+\dfrac{1}{53}-\dfrac{1}{45}-\dfrac{1}{47}\right)=0\\ \Leftrightarrow x-100=0\left(\dfrac{1}{55}+\dfrac{1}{53}-\dfrac{1}{45}-\dfrac{1}{47}\ne0\right)\\ \Rightarrow x=100\)