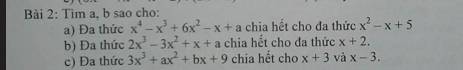Question

Answer 1

a.

$f(x)=x^4-x^3+6x^2-x+a=x^2(x^2-x+5)+x^2-x+a$

$=x^2(x^2-x+5)+(x^2-x+5)+(a-5)=(x^2+x-5)(x^2+1)+(a-5)$

Để $f(x)\vdots x^2-x+5$ thì $a-5=0$

$\Leftrightarrow a=5$

b.

$f(x)=2x^3-3x^2+x+a=2x^2(x+2)-7x(x+2)+15x+a$

$=2x^2(x+2)-7x(x+2)+15(x+2)+(a-30)$

$=(x+2)(2x^2-7x+15)+(a-30)$

Để $f(x)\vdots x+2$ thì $a-30=0\Leftrightarrow a=30$

c.

$f(x)=3x^3+ax^2+bx+9\vdots x+3$ và $x-3$ khi mà:
$f(3)=f(-3)=0$ (theo định lý Bê-du)

$\Leftrightarrow 3.3^3+a.3^2+3b+9=3(-3)^3+a(-3)^2+b(-3)+9=0$

$\Leftrightarrow 3a+b=-30$ và $3a-b=24$

$\Rightarrow a=-1; b=-27$