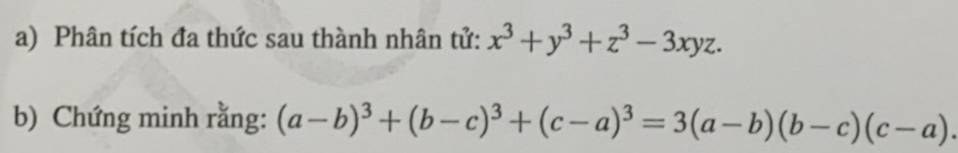`a, x^3 + y^3 + z^3 - xyz`
`= (x+y+z)(x^2 + y^2 + z^2 - xy - yz - xz)`.
Bài 2:
`a^3 - 3a^2b + 3ab^2 - b^3 + b^3 - 3b^2c + 3bc^2 - c^3 + c^3 - 3c^2a + 3ca^2 - a^3`.
`=3(ab^2 + bc^2 + ca^2 - a^2b - b^2c - c^2a)`
`= 3(a-b)(b-c)(c-a)`.
a) \(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\\ =\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\\ =\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
b) Áp dụng câu a: đặt \(\left\{{}\begin{matrix}a-b=x\\b-c=y\\c-a=z\end{matrix}\right.\Rightarrow x+y+z=0\)
\(\left(a-b\right)^3+\left(b-c\right)^3+\left(c-a\right)^3-3\left(a-b\right)\left(b-c\right)\left(c-a\right)\\ =x^3+y^3+z^3-3xyz\\ =\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\\ =0\)
\(\Rightarrow\left(a-b\right)^3+\left(b-c\right)^3+\left(c-a\right)^3=3\left(a-b\right)\left(b-c\right)\left(c-a\right)\)
a) \(x^3+y^3+z^3-3xyz\)
\(=\left[\left(x+y\right)^3+z^3\right]-\left[3xy\left(x+y\right)+3xyz\right]\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2-3xy\right]\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)
b) Ta có:
\(VT=\left(a-b\right)^3+\left(b-c\right)^3+\left(c-a\right)^3\)
\(=\left[\left(a-b\right)^3+\left(b-c\right)^3\right]+\left(c-a\right)^3\)
\(=\left(a-b+b-c\right)^3-3\left(a-b\right)\left(b-c\right)\left(a-b+b-c\right)+\left(c-a\right)^3\)
\(=\left(a-c\right)^3-3\left(a-b\right)\left(b-c\right)\left(a-c\right)+\left(c-a\right)^3\)
\(=\left(a-c\right)^3+3\left(a-b\right)\left(b-c\right)\left(c-a\right)-\left(a-c\right)^3\)
\(=3\left(a-b\right)\left(b-c\right)\left(c-a\right)=VP\) (đpcm)