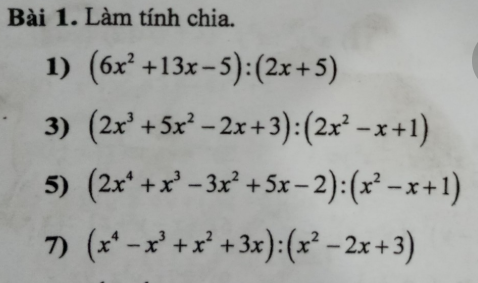\(1,=\left(6x^2+15x-2x-5\right):\left(2x+5\right)\\ =\left(2x+5\right)\left(3x-1\right):\left(2x+5\right)\\ =3x-1\\ 3,=\left(2x^3-x^2+x+6x^2-3x+3\right):\left(2x^2-x+1\right)\\ =\left(2x^2-x+1\right)\left(x+3\right):\left(2x^2-x+1\right)\\ =x+3\\ 5,=\left(2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x-2\right):\left(x^2-x+1\right)\\ =\left(x^2-x+1\right)\left(2x^2+3x-2\right):\left(x^2-x+1\right)\\ =2x^2+3x-2\)
\(7,=\left(x^4-2x^3+3x^2+x^3-2x^2+3x\right):\left(x^2-2x+3\right)\\ =\left(x^2-2x+3\right)\left(x^2+1\right):\left(x^2-2x+3\right)\\ =x^2+1\)
Đúng 0
Bình luận (0)
