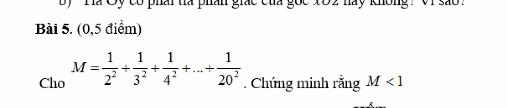Ta có: \(\dfrac{1}{2^2}< \dfrac{1}{1.2}\) ; \(\dfrac{1}{3^2}< \dfrac{1}{2.3}\) ; \(\dfrac{1}{4^2}< \dfrac{1}{3.4}\) ;....; \(\dfrac{1}{20^2}< \dfrac{1}{19.20}\)
⇒ M = \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{20^2}\) \(< \) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{19.20}\)
⇒ M \(< \) \(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
⇒ M \(< \) \(1-\dfrac{1}{20}\) \(< \) \(1\)
Vậy M = \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{20^2}\) \(< \) \(1\)