a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
b) Xét (O) có
OG là một phần đường kính
EC là dây
G là trung điểm của EC
Do đó: OG⊥EC(Định lí đường kính vuông góc với dây)
Ta có: OA là đường trung trực của BC(cmt)
nên OA⊥BC tại D
Xét ΔAGO vuông tại G và ΔHDO vuông tại D có
\(\widehat{AOG}\) chung
Do đó: ΔAGO∼ΔHDO(g-g)



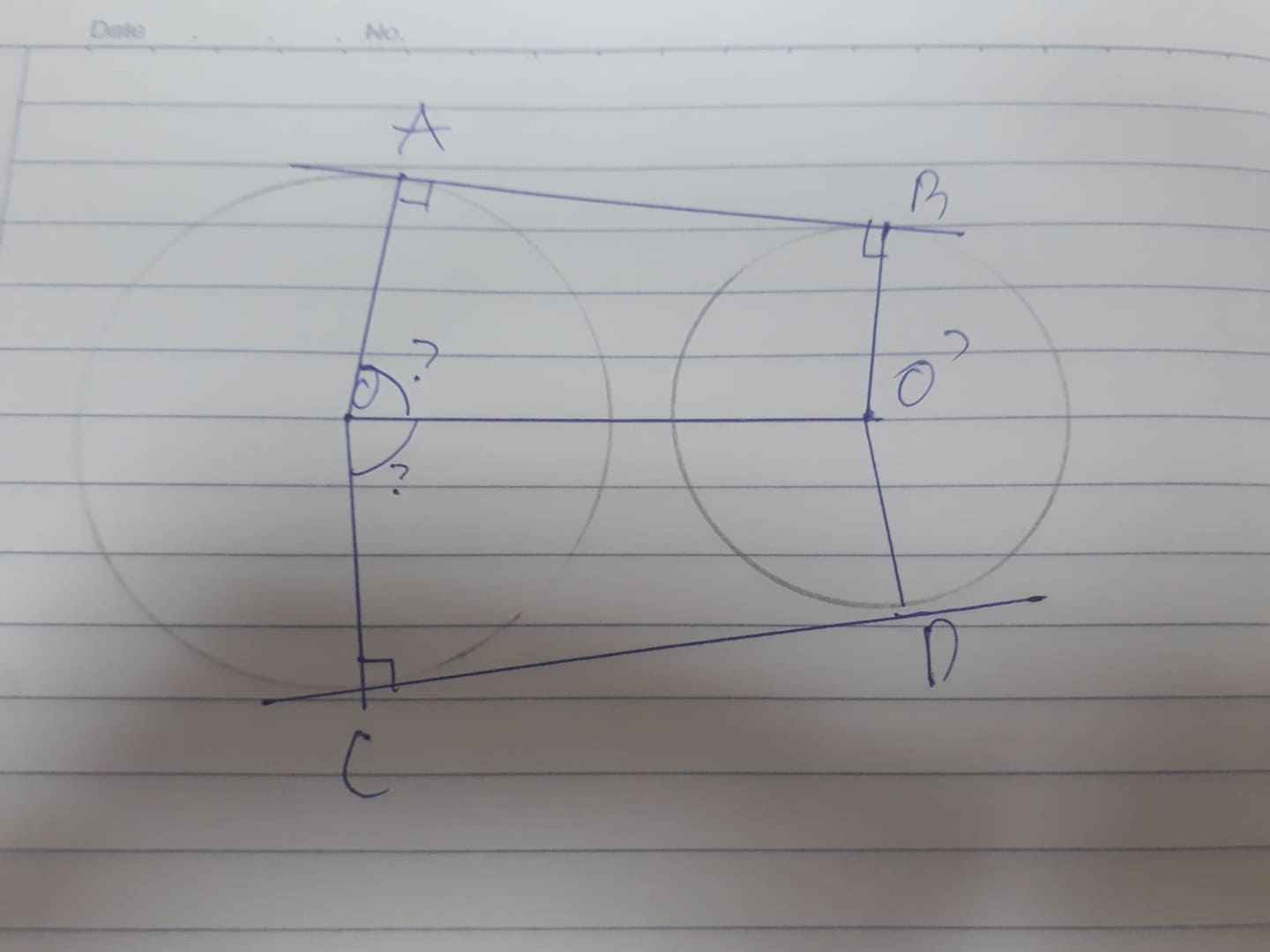 ai chứng minh hộ mik 2 góc ? trên kia bằng nhau hô j mik với
ai chứng minh hộ mik 2 góc ? trên kia bằng nhau hô j mik với