Toán

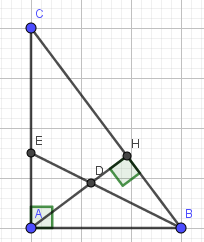
a) Ta có:

\(\widehat{BAH}+\widehat{ABC}=90^0\)

\(\widehat{BCA}+\widehat{ABC}=90^0\)

\(\Rightarrow\widehat{BAH}=\widehat{BCA}\)

\(\Rightarrow\widehat{BAD}=\widehat{BCE}\)

Do \(BE\) là phân giác của \(\widehat{ABC}\left(gt\right)\)

\(\widehat{ABE}=\widehat{CBE}\)

\(\Rightarrow\widehat{ABD}=\widehat{CBE}\)

Xét \(\Delta BAD\) và \(\Delta BCE\) có:

\(\widehat{BAD}=\widehat{BCE}\left(cmt\right)\)

\(\widehat{ABD}=\widehat{CBE}\left(cmt\right)\)

\(\Rightarrow\Delta BAD\sim\Delta CBE\left(g-g\right)\)

Do \(\widehat{CBE}=\widehat{ABE}\left(cmt\right)\)

\(\Rightarrow\widehat{HBD}=\widehat{ABE}\)

Xét hai tam giác vuông: \(\Delta BHD\) và \(\Delta BAE\) có:

\(\widehat{HBD}=\widehat{ABE}\left(cmt\right)\)

\(\Rightarrow\Delta BHD\sim\Delta BAE\left(g-g\right)\)

b) Do \(\Delta BAD\sim\Delta CBE\left(cmt\right)\)

\(\Rightarrow\dfrac{BA}{BE}=\dfrac{DA}{EC}\) (1)

Do \(\Delta BHD\sim\Delta BAE\) (cmt)

\(\Rightarrow\dfrac{BD}{BE}=\dfrac{DH}{EA}\) (2)

Từ (1) và (2) \(\Rightarrow\dfrac{DA}{EC}=\dfrac{DH}{EA}\)

\(\Rightarrow\dfrac{DH}{DA}=\dfrac{EA}{EC}\)

c) \(\Delta ABC\) vuông tại A (gt)

\(\Rightarrow BC^2=AB^2+AC^2\left(Pythagore\right)\)

\(\Rightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)

\(\Rightarrow AC=5\left(cm\right)\)

Theo công thức tính diện tích tam giác, ta có:

\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)

\(\Rightarrow AH.BC=AB.AC\)

\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=2,4\left(cm\right)\)

\(\Delta AHB\) vuông tại H

\(\Rightarrow AB^2=AH^2+HB^2\left(Pythagore\right)\)

\(\Rightarrow HB^2=AB^2-AH^2=3^2-\left(2,4\right)^2=3,24\)

\(\Rightarrow HB=1,8\left(cm\right)\)

\(\Rightarrow HC=BC-HB=5-1,8=3,2\left(cm\right)\)

Đặt \(A=\sqrt[3]{9+\sqrt{80}}+\sqrt[3]{9-\sqrt{80}}\)

=>\(A^3=9+\sqrt{80}+9-\sqrt{80}+3\cdot\sqrt[3]{\left(9+\sqrt{80}\right)\left(9-\sqrt{80}\right)}\cdot A\)

=>\(A^3=18+3A\)

=>\(A^3-3A-18=0\)

=>\(A^3-3A^2+3A^2-9A+6A-18=0\)

=>\(\left(A-3\right)\left(A^2+3A+6\right)=0\)

mà \(A^2+3A+6=\left(A+\dfrac{3}{2}\right)^2+\dfrac{15}{4}>0\forall A\)

nên A-3=0

=>A=3

a: Xét (O) có

ΔABC nội tiếp

BC là đường kính

Do đó: ΔABC vuông tại A

=>BA\(\perp\)DC tại A

Xét ΔDBC vuông tại B có BA là đường cao

nên \(DA\cdot DC=DB^2\)

b: Xét tứ giác DBOE có \(\widehat{DBO}+\widehat{DEO}=90^0+90^0=180^0\)

nên DBOE là tứ giác nội tiếp

=>D,B,O,E cùng thuộc một đường tròn

Xét (O) có

DB,DE là các tiếp tuyến

Do đó: DB=DE

=>D nằm trên đường trung trực của BE(1)

Ta có: OB=OE

=>O nằm trên đường trung trực của BE(2)

Từ (1),(2) suy ra DO là đường trung trực của BE

=>DO\(\perp\)BE tại I

Xét ΔDBO vuông tại B có BI là đường cao

nên \(DI\cdot DO=DB^2\)

=>\(DI\cdot DO=DA\cdot DC\)

c: Gọi F là giao điểm của CE và BD

Ta có: EM\(\perp\)BC

FB\(\perp\)BC

Do đó: EM//FB

Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>BE\(\perp\)CF tại E

=>ΔBEF vuông tại E

Ta có: \(\widehat{DBE}+\widehat{DFE}=90^0\)(ΔFEB vuông tại E)

\(\widehat{DEB}+\widehat{DEF}=\widehat{FEB}=90^0\)

mà \(\widehat{DBE}=\widehat{DEB}\)(ΔDBE cân tại D)

nên \(\widehat{DFE}=\widehat{DEF}\)

=>DE=DF

mà DE=DB

nên DB=DF(3)

Xét ΔCDB có MG//DB

nên \(\dfrac{MG}{DB}=\dfrac{CG}{CD}\left(4\right)\)

Xét ΔCDF có EG//DF

nên \(\dfrac{EG}{DF}=\dfrac{CG}{CD}\left(5\right)\)

Từ (3),(4),(5) suy ra MG=EG

=>G là trung điểm của ME

Xét ΔEBM có

I,G lần lượt là trung điểm của EB,EM

=>IG là đường trung bình của ΔEBM

=>IG//BM

=>IG//BC

1: Thay x=16 vào A, ta được:

\(A=\dfrac{16+3}{\sqrt{16}-2}=\dfrac{19}{4-2}=\dfrac{19}{2}\)

2: \(B=\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{3\sqrt{x}+6}{x-4}\)

\(=\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{3\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}-2}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)

3: \(\dfrac{A}{B}=\dfrac{x+3}{\sqrt{x}-2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{x+3}{\sqrt{x}}\)

\(\dfrac{A}{B}-3=\dfrac{x+3-3\sqrt{x}}{\sqrt{x}}=\dfrac{x-3\sqrt{x}+\dfrac{9}{4}+\dfrac{3}{4}}{\sqrt{x}}\)

=>\(\dfrac{A}{B}-3=\dfrac{\left(\sqrt{x}-\dfrac{3}{2}\right)^2+\dfrac{3}{4}}{\sqrt{x}}>0\) với mọi x thỏa mãn ĐKXĐ

=>\(\dfrac{A}{B}>3\)

2: \(\Omega=\left\{44;55;66;45;46;54;56;64;65\right\}\)

=>\(n\left(\Omega\right)=9\)

Gọi A là biến cố "Số được viết có hai chữ số khác nhau"

=>A={45;46;54;56;64;65}

=>n(A)=6

=>\(P_A=\dfrac{6}{9}=\dfrac{2}{3}\)

a) ∆ = (5k)² - 4.(-1).4 = 25k² + 16 > 0 với mọi k ∈ R

Theo định lí Viét, ta có:

x₁ + x₂ = 5k

x₁x₂ = -4

Ta có:

x₁² + x₂² + 6x₁x₂ = 9

(x₁ + x₂)² - 2x₁x₂ + 6x₁x₂ = 9

(x₁ + x₂)² + 4x₁x₂ = 9

(5k)² + 4.(-4) = 9

25k² - 16 = 9

25k² = 9 + 16

25k² = 25

k² = 25 : 25

k² = 1

k = -1 hoặc k = 1

Vậy k = -1; k = 1 thì phương trình đã cho có hai nghiệm thỏa mãn yêu cầu đề bài