Giải và biện luận phương trình :
mx2 - 2 = 4x + m (m là tham số , x là ẩn )
Giải và biện luận theo tham số m các phương trình sau
m x 2 + ( 2 m - 1 ) x + m - 2 = 0
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
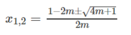
giải và biện luận phương trình
2(mx+5) + 5(x+m) = m
( với m là tham số , x là ẩn)
Giải và biện luận các phương trình sau (với m là tham số):
a) mx – x – m + 2 = 0
\(b) m^2x + 3mx – m^2 + 9 = 0 \)
\(c) m^3x – m^2 - 4 = 4m(x – 1)\)
2) Cho phương trình ẩn x: . Hãy xác định các giá trị của k để phương trình trên có nghiệm x = 2.
\(mx-x-m+2=0\)
\(x\left(m-1\right)=m-2\)
Nếu m=1 ⇒ \(0x=-1\) (vô nghiệm)
Nếu m≠1 ⇒ \(x=\dfrac{m-2}{m-1}\)
Vậy ...
Giải và biện luận phương trình ẩn x và tham số m :
\(\left|x+m\right|=2+\left|x-m\right|\)
\(\left|x+m\right|=2+\left|x-m\right|\) ( Hai vế đều dương nên bình phương hai vế không cần điều kiện)
\(\Leftrightarrow x^2+2mx+m^2=4+4\left|x-m\right|+x^2-2mx+m^2\)
\(\Leftrightarrow4mx=4+4\left|x-m\right|\)
\(\Leftrightarrow mx=1+\left|x-m\right|\)
\(\Leftrightarrow mx-1=\left|x-m\right|\) (1) Điều kiện: \(mx-1\ge0\) (*)
Với: \(mx-1\ge0\)
\(\left(1\right)\Leftrightarrow m^2x^2-2mx+1=x^2-2mx+m^2\)
\(\Leftrightarrow m^2x^2+1=x^2+m^2\)
\(\Leftrightarrow\left(m^2-1\right)x^2=m^2-1\) (2)
TH1: \(\left(m^2-1\right)=0\Leftrightarrow\orbr{\begin{cases}m=1\\m=-1\end{cases}}\)
+ Với \(m=1\) thì \(\hept{\begin{cases}\left(\text{*}\right)\Leftrightarrow x\ge1\\\left(2\right)\Leftrightarrow0=0\left(\text{luôn đúng với mọi x}\right)\end{cases}}\Leftrightarrow x\ge0\)
+ Với \(m=-1\) thì \(\hept{\begin{cases}\left(\text{*}\right)\Leftrightarrow x\le-1\\\left(2\right)\Leftrightarrow0=0\left(\text{luôn đúng với mọi x }\right)\end{cases}\Leftrightarrow}x\le-1\)
TH2: Với \(m=0\) thì \(\left(\text{*}\right)\Leftrightarrow0-1\ge0\) ( vô lý ) => vô nghiệm
TH3: \(\left(m^2-1\right)\ne0\Leftrightarrow\orbr{\begin{cases}m\ne1\\m\ne-1\end{cases}}\)
+ Với: \(\hept{\begin{cases}m< 0\\m\ne-1\end{cases}}\) thì \(\hept{\begin{cases}\left(\text{*}\right)\Leftrightarrow x\le\frac{1}{m}\\\left(2\right)\Leftrightarrow x^2=\frac{m^2-1}{m^2-1}=1\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(\text{*}\right)\Leftrightarrow x\le\frac{1}{m}< 0\\x=\text{1 hoặc -1}\end{cases}}\Leftrightarrow x=-1\)
+ Với: \(\hept{\begin{cases}m>0\\m\ne1\end{cases}}\) thì \(\hept{\begin{cases}\left(\text{*}\right)\Leftrightarrow x\ge\frac{1}{m}\\\left(2\right)\Leftrightarrow x^2=\frac{m^2-1}{m^2-1}=1\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(\text{*}\right)\Leftrightarrow x\ge\frac{1}{m}>0\\\left(2\right)\Leftrightarrow x^2=\text{1 hoặc -1}\end{cases}}\Leftrightarrow x=1\)
Tự kết luận nhé
\(\left|x+m\right|=2+\left|x-m\right|\)
\(\Leftrightarrow\left(\left|x+m\right|\right)^2=\left(2+\left|x-m\right|\right)^2\)
\(\Leftrightarrow x^2+2mx+m^2=m^2-2mx-4m+x^2+4x+4\)
\(\Leftrightarrow4mx+4m-4x-4=0\)
\(\Leftrightarrow4\left(m-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(x+1\right)=0\)
.....
You phạm một sai lầm trầm trọng , chú ý đoạn này :
\(\left(2+\left|x-m\right|\right)^2=\left(x-m\right)^2+4\left|x-m\right|+4\)
Giải và biện luận phương trình với m là tham số : x^2-x+m=0
Xét phương trình \(\left(m-1\right)x-m+5=0\) ( ẩn x, tham số m )
a) Tìm m để x = -3 là nghiệm của phương trình.
b) Chứng tỏ với m = 1 phương trình vô nghiệm
c) Giải và biện luận phương trình.
a) x=3 có: 3(m-1) -m+5 =0
3m-3-m+5 =0 => m = -1
b) nếu m=1 có: (m-1)x = 0 => (m-1)x -m +5 = 0 => 4=0 vô lý
c) (m-1)x -m+5 =0 => x = (m-5)/(m-1)
+ nếu m=1 vô nghiệm
+ m khác 1 pt có nghiệm x =(m-5)/(m-1)
chỉ biện luận mỗi vậy thôi hả ???????
.cho phương trình ẩn x:ax2+(b-m)x+c=0 .Viết chương trình :
a) giải phương trình với hệ số a=0.
b)biện luận nghiệm của phương trình theo tham số m.
Câu 1: Giải và biện luận bất phương trình \(m^2x+m\ge2-4x\)
Câu 2: Tìm giá trị thực của tham số m để bất phương trình \(m\left(2x-1\right)\ge2x-1\) có tập nghiệm là \([1;+\infty)\)
1.
\(\Leftrightarrow\left(m^2+4\right)x\ge2-m\)
Do \(m^2+4>0\) ; \(\forall m\)
\(\Rightarrow x\ge\dfrac{2-m}{m^2+4}\)
2.
\(\Leftrightarrow2mx-2x\ge m-1\Leftrightarrow2\left(m-1\right)x\ge m-1\)
- Với \(m>1\Rightarrow m-1>0\)
\(\Rightarrow x\ge\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\ge\dfrac{1}{2}\) \(\Rightarrow D=[\dfrac{1}{2};+\infty)\)
- Với \(m< 1\Rightarrow m-1< 0\Rightarrow x\le\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\le\dfrac{1}{2}\) \(\Rightarrow D=(-\infty;\dfrac{1}{2}]\)
- Với \(m=1\Leftrightarrow0\ge0\Rightarrow D=R\)
Quan sát 3 TH ta thấy không tồn tại m để tập nghiệm của BPT là \([1;+\infty)\)
Giải và biện luận phương trình:
x-a^2x-b^2/b^2-x^2+a=x^2/x^2-b^2 với a,b là tham số; x là ẩn số
(Đề 1)
mày éo viết được cái đề hẳn họi à ????