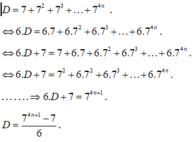cm: 1/72-1/74+...+1/74n-1-1/74n+...+1/798-1/7100<1/50
VK
Những câu hỏi liên quan
Chứng minh rằng
71 + 72 + 73+ 74 + ......... +74n-1 +74n chia hết cho 400
Tìm chữ số tận cùng các số sau
a) 91991
b) 2335
c) 7430
d) 74n-1-1
CMR:
a)74n-1 chia hết cho 5
b)34n+1+2 chia hết cho 5
c)92n+1+1 chia hết cho 10
d)24n+2+1 chia hết cho 5
1)E = 5 + 52 + 53+ ... + 520
CMR E : 7
2) F = 7 + 72+ 73 + 74 + ... + 7100
CMR F : 8
F = 7 + 72 + 73 + 74 + ..... + 7100
F= 7+(1+7)+73+(1+7)+...+799+(1+7)
F = 7x8+73x8+...+799x8
F= 8x(7+73+...+799)
mà 8 chia hết 8 => 8(7+73+...+799) chia hết 8
Vậy F chia hết cho 8
Đúng 3
Bình luận (0)
2)
\(F=7+7^2+7^3+7^4+...+7^{100}\\ F=7\cdot\left(1+7\right)+7^3\cdot\left(1+7\right)+.....+7^{99}\cdot\left(1+7\right)\\F=7\cdot8+7^3\cdot8+.....+7^{99}\cdot8\\ F=8\cdot\left(7+7^3+....+7^{99}\right)\\ =>F⋮8\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm chữ số tận cùng của:
e. E = 24n+2 +1
f. F = 74n −1
g. 1+ 9 + ...+ 92020
h. 1
33 + 233 +!+ 8933
Tính tổng: D = 7 + 7 2 + 7 3 + … 7 4 n
chung minh rang moi so n de: a) 74n - 1 chia het cho 5
b) 34n + 1 + 2 chia het cho 5
c) 24n + 1 + 3 chia het cho 5
d) 92n + 1 + 1 chia het cho 10
viết lại đề cho chuẩn
nhìn mình chẳng hiểu n là số mũ hay là nhân, hay có gạch trên đầu...
Đúng 0
Bình luận (0)
à
n la so mu nha ban giai mik voi
Đúng 0
Bình luận (0)
a)
\(74^n-1\) đề sai vơi n lẻ không chia hết cho 5 xem lại và viết cho chuẩn đi
Đúng 0
Bình luận (0)
Mn giải cho e ặ !
M = 7 + 72 + 73 + 74 + ..... + 7100
M chia hết cho 8
\gấp ặ/
M = 7 + 72 + 73 + 74 + ..... + 7100
M = 7+(1+7)+73+(1+7)+...+799+(1+7)
M = 7x8+73x8+...+799x8
M = 8x(7+73+...+799)
mà 8 chia hết 8 => 8(7+73+...+799) chia hết 8
Vậy M chia hết cho 8
Đúng 1
Bình luận (0)
Chiều cao
52 cm
26 cm
74 cm
55 cm
56 cm
Độ dài dáy 1
45cm
88 cm
65 cm
72 cm
Độ dài dáy 2
65 cm
35 cm
63 cm
Diện tích hình thang
780 cm2
452 cm2
784 cm2
Đọc tiếp
| Chiều cao | 52 cm | 26 cm | 74 cm | 55 cm | 56 cm |
| Độ dài dáy 1 | 45cm | 88 cm | 65 cm | 72 cm | |
| Độ dài dáy 2 | 65 cm | 35 cm | 63 cm | ||
| Diện tích hình thang | 780 cm2 | 452 cm2 | 784 cm2 |
dòng diện tích hình thang phải cách ra bạn êy
Đúng 0
Bình luận (0)
1) B= 1+3+32+...+31999+32000
2) C= 1+4+42+...+499+4100
3) D= 72+73+74+...+72019+72020
Tính các tổng hộ mình nhé.
\(1)B=1+3+3^2+...+3^{1999}+3^{2000}\\3B=3+3^2+3^3+...+3^{2000}+3^{2001}\\3B-B=3+3^2+3^3+...+3^{2000}+3^{2001}-(1+3+3^2+...+3^{1999}+3^{2000})\\2B=3^{2001}-1\\\Rightarrow B=\dfrac{3^{2001}-1}{2}\\---\)
\(2)C=1+4+4^2+...+4^{99}+4^{100}\\4C=4+4^2+4^3+...+4^{100}+4^{101}\\4C-C=4+4^2+4^3+...+4^{100}+4^{101}-(1+4+4^2+....+4^{99}+4^{100})\\3C=4^{101}-1\\\Rightarrow C=\dfrac{4^{101}-1}{3}\)
#\(Toru\)
Đúng 1
Bình luận (2)
1) \(B=1+3+3^2+...+3^{1999}+3^{2000}\)
\(3B=3\cdot\left(1+3+3^2+...+3^{2000}\right)\)
\(3B=3+3^2+...+3^{2001}\)
\(3B-B=3+3^2+3^3+...+3^{2001}-1-3-3^2-...-3^{2000}\)
\(2B=3^{2001}-1\)
\(B=\dfrac{3^{2001}-1}{2}\)
2) \(C=1+4+4^2+...+4^{100}\)
\(4C=4\cdot\left(1+4+4^2+...+4^{100}\right)\)
\(4C=4+4^2+4^3+...+4^{101}\)
\(4C-C=4+4^2+4^3+...+4^{201}-1-4-4^2-....-4^{100}\)
\(3C=4^{101}-1\)
\(C=\dfrac{4^{101}-1}{3}\)
Đúng 0
Bình luận (2)
Mình cho bạn công thức tổng quát để sau này tiện áp dụng nhé:
\(A=1+a^1+a^2+...+a^n\)
\(\Rightarrow A=\dfrac{a^{n+1}-1}{a-1}\)
Đúng 0
Bình luận (0)