Tìm max:\(1-5.x^2-y^2-4xy+2x\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
TÌM MAX CỦA \(A=-x^2-y^2+4xy+2x+2y\)
1. Tìm max hoặc min:
a. A = x^2 - 5x - 1
b. B = 1/4x - x + 5.
c. C = x^2 - 4xy + 7y^2 - 2y +3
d. D = 5x^2 - xy + 1/24y^2 + 2x - 1
e. E = x^2 - 3xy + y - 2y - 1
2. Tìm x:
a. ( 2x - 3 )^2 - ( 4x + 1 ).( 4x - 1 ) = ( 2x - 1 ).( 3 - 7x )
b. 1/16x^2 - ( 3x + 5 ) = 0
c. 4.( x - 3 ) - ( x + 2 ) = 0
1. Tính
a) 2xy(3xy+2xy^2)
b) (2x-1)(x^2+2x+4)-(x^2-3x)*2x
2. Phân tích đa thức thành nhân tử
a) 4x^3y-8x^2y^2+4xy^3
b) 2xy+3xz+6y^2+xz
c) y^2-4x-4xy+4x^2+2y
3. Thực hiện phép chia
(6x^3-7x^2-x+z):(2x+1)
4. Tìm a để đa thức 2x^3+5x^2-2x+a chia hết đa thức 2x^2-x+1
5. Tìm max của biểu thức A=-2x^2+x-z
Tìm Max của A=2-5x2-y2-4xy+2x
A = - ( 4x2 + 4xy + y2) - (x2 -2x +1) + 3 = 3 - (2x + y)2 - (x - 1)2 <= 3
Vậy max là 3 khi x = 1; y = -2
Đúng 0
Bình luận (0)
1. tìm Min , Max
a, A= x^2-1+1
b,B= 3x^2-5+7
c,C= -2x^2 - x +1
d= x^2 +y^2 -2x +6y +12
e, E= -2x^2 +x
f= x^2+5y^2 - 4xy +6x -14y+15
đề câu a, b có sai ko vậy pn,mk thấy sai
Đúng 0
Bình luận (0)
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
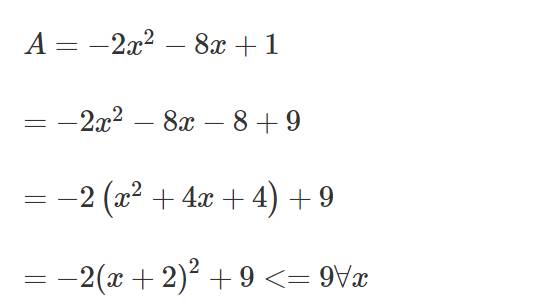
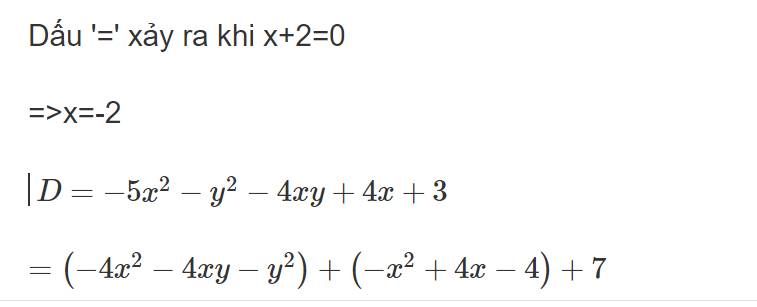
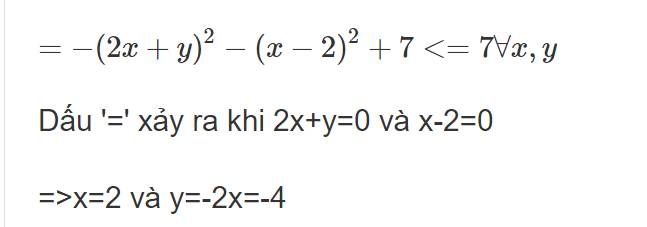
Đúng 0
Bình luận (0)
Tìm Max
C= 15+2x+5y-x2-5y2
D= -5x2-y2+2xy-2x-2y+1
2) Tìm Min
D = x2 + xy +y2
G = (x+3y-5)2 - 6xy + 26
H = 4x2 + y2 - 4xy + 4x - 2y + 2
L = x2 + 5y2 + 4xy - 2x - 8y + 3
Các bạn làm được câu nào thì làm nha. Bạn nào làm được hết thì tốt quá ạ!!! Mình cảm ơn !!!
1)Tìm x,y để:-5-3y chia hết cho 2+4y
2)Tìm x,y để:2x+3y+4xy=-5
Tìm min hoặc max của bthc sau: 2x2-4xy+4y2+2x+5
\(2x^2-4xy+4y^2+2x+5=\left(x^2-4xy+4y^2\right)+\left(x^2+2x+1\right)+4=\left(x-2y\right)^2+\left(x+1\right)^2+4\)
\(\left(x-2y\right)^2\ge0;\left(x+1\right)^2\ge0\Rightarrow\left(x-2y\right)^2+\left(x+1\right)^2\ge0\)
\(\Rightarrow\left(x-2y\right)^2+\left(x+1\right)^2+4\ge4\)
vậy max của biểu thức trên = 4
Đúng 0
Bình luận (0)



