A=92001.92003 và B=22002^2
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
cho A=1+2+22+...22002
B=22003
so sánh A vs B
Ta có:
\(A=1+2+2^2+...+2^{2002}\)
\(2A=2+2^2+2^3+...+2^{2003}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+....+2^{2002}\right)\)
\(A=2^{2003}-1\)
Mà: \(2^{2003}=2^{2003}\)
\(\Rightarrow2^{2003}-1< 2^{2003}\)
\(\Rightarrow A< B\)
Đúng 2
Bình luận (0)
Cho A 4 + 22 + 23 + 24 + ... + 22002. Chứng minh rằng A là một luỹ thừa của 2.
Đọc tiếp
Cho A = 4 + 22 + 23 + 24 + ... + 22002. Chứng minh rằng A là một luỹ thừa của 2.
A=4+22+23+....+220
2A=8+23+24+...+221
=> A+2A-A = (8+23+24+...+221) - (4+22+23+....+220)
=>A=221+8 - (22+4)=221
=>A là 1 lũy thừa của 2
Đúng 0
Bình luận (0)
Cho A = 4 + 22 + 23 + 24 + ... + 22002. Chứng minh rằng A là một luỹ thừa của 2
A= 4+22+23+....+220
2A= 8+23+24+...+221
A + 2A -A = (8+2^3+2^4+...+2^21) - (4+2^2+2^3+....+2^20)
A= 2^21+8 - (2^2+4)=2^21
Vậy A là 1 lũy thừa của 2
Đúng 1
Bình luận (0)
Cho A=4+22+23+24+...+22002.Chứng minh rằng A là một luỹ thừa của 2
Giúp đi nhanh k cho
Cho A=4+22+23+24+...+22002. Chứng minh rằng A là một luỹ thừa của 2
giúp với nhanh kich cho
vậy nên mình mới hỏi chứ bỏ 23 đi thì mình tự giải cũng đc
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
H24
23 tháng 9 2021 lúc 10:59
4. a) Tính tổng: S = 12 + 22 + 32 + …+ 20042
b) Chứng minh: P = 12002 + 22002+…+20042002 không là số chính phương.
H24
18 tháng 9 2021 lúc 14:11
4. a) Tính tổng: S = 12 + 22 + 32 + …+ 20042
b) Chứng minh: P = 12002 + 22002+…+20042 không là số chính phương.
a) có tất cả số hạng là:
(20042-12):10+1=2004
tổng là:
\(\dfrac{\text{(20042+12).2004}}{2}\)\(=20094108\)
Đúng 0
Bình luận (0)
Chứng minh rằng:
22002 __ 4 chia hết cho 31
Giải các phương trình sau
x
-
10
1994
+
x
-
8
1996
+
x
-
6
1998
+
x
-
4
2000
+
x...
Đọc tiếp
Giải các phương trình sau x - 10 1994 + x - 8 1996 + x - 6 1998 + x - 4 2000 + x - 2 2002 = x - 2002 2 + x - 2000 4 + x - 1998 8 + x - 1994 10
Ta có: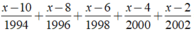
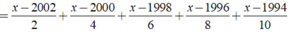
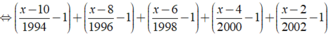
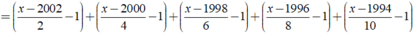
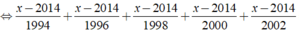
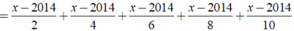
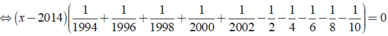
⇒ x - 2014 = 0 ⇔ x = 2014.
Vậy phương trình đã cho có nghiệm là x = 2014.
Đúng 0
Bình luận (0)