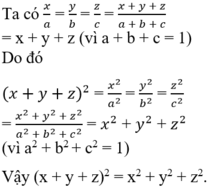Cho a+b+c = a2+b2+c2=1 và x:y:z=a:b:c. CMR : (x+y+z)2=x2+y2+z2
H24
Những câu hỏi liên quan
Cho a/x+b/y+C/z=2 và x/a+y/b+z/c=0 . Chứng minh A=x2/a2+y2/b2+z2/c2=1
Cho a + b + c = a2 + b2 + c2 = 1 và x : y : z = a : b : c.
Chứng minh rằng: (x + y + z)2 = x2 + y2 + z2.
Cho a+b+c = a2+b2+c2=1 và \(\dfrac{x}{a}\) = \(\dfrac{y}{b}\) = \(\dfrac{z}{c}\) và ( a,b,c ≠ 0 )
Hãy chứng minh (x+y+z)2=x2+y2+z2
Có: \(a+b+c=1\Leftrightarrow\left(a+b+c\right)^2=1\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}\)
\(\Rightarrow\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}=\dfrac{\left(x+y+z\right)^2}{\left(a+b+c\right)^2}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\)
\(\Rightarrow\left(x+y+z\right)^2=x^2+y^2+z^2\) (do \(\left(a+b+c\right)^2=a^2+b^2+c^2=1\))
Đúng 0
Bình luận (0)
Các số thực a,b,c,x,y,z thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
c
+
4
0
và
x
2
+
y
2
+
z
2
-
4
x
+
4
y
+
4...
Đọc tiếp
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
![]()
![]()
![]()
![]()
Cho a,b,c,x,y,z thỏa mãn a+b+c=a2+b2+c2=1 và x/a=y/b=z/c.Chứng minh rằng:x2+y2+z2=(x+y+z)2
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) ⇒ \(\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{a^2}\) = \(\dfrac{y^2}{b^2}\) = \(\dfrac{z^2}{c^2}\) = \(\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\) = \(\dfrac{x^2+y^2+z^2}{1}\) = \(x^2+y^2+z^2\) (1)
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}\) = \(\dfrac{x+y+z}{1}\) = \(x+y+z\)
\(\dfrac{x}{a}\) = \(x+y+z\) ⇒ \(\dfrac{x^2}{a^2}\) = (\(x+y+z\))2 (2)
Từ (1) và (2) ta có :
\(\dfrac{x^2}{a^2}\) = \(x^2\) + y2 + z2 = ( \(x+y+z\))2 (đpcm)
Đúng 1
Bình luận (0)
⇒
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
= = = = =
Bài 3 Chứng minh rằng với a, b, c, x, y, z (trong đó xyz 6 0) thỏa mãn (a2 + b2 + c2)(x2 + y2 + z2) (ax + by + cz)2 thì a/x b/y c/z.
Đọc tiếp
Bài 3 Chứng minh rằng với a, b, c, x, y, z (trong đó xyz 6= 0) thỏa mãn (a2 + b2 + c2)(x2 + y2 + z2) = (ax + by + cz)2
thì a/x =b/y =c/z.
cho a+b+c =a2+b2+c2=1 và x/a=y/b=z/c (a,b,c khác 0 )
hãy cm:(x+y+y)2=x2+y2+z
Áp dụng tính chất các dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}=\dfrac{x+y+z}{1}\)
\(x=a\left(x+y+z\right)=x^2=a^2.\left(x+y+z\right)^2\)
\(y=b\left(x+y+z\right)=y^2=b^2\left(x+y+z\right)^2\)
\(z=c\left(x+y+z\right)=z^2=c^2.\left(x+y+z\right)^2\)
\(\Rightarrow x^2+y^2+z^2=a^2\left(x+y+z\right)^2+b^2\left(x+y+z\right)^2+c^2\left(x+y+z\right)^2\)
\(=\left(x+y+z\right)^2\left(a^2+b^2+c^2\right)=\left(x+y+z\right)^2\) (do \(a^2+b^2+c^2=1\))
Đúng 1
Bình luận (1)
Cho a + b + c a2 + b2 + c2 1 vàdfrac{x}{a}dfrac{y}{b}dfrac{z}{c}( a≠0,b≠0,c≠0 )Chứng minh rằng (x+y+z)2x2+y2+z2Giúp mình với ạ, mai mình thi rồi !!!!
Đọc tiếp
Cho a + b + c = a2 + b2 + c2 = 1 và\(\dfrac{x}{a}\)=\(\dfrac{y}{b}\)=\(\dfrac{z}{c}\)( a≠0,b≠0,c≠0 )
Chứng minh rằng (x+y+z)2=x2+y2+z2
Giúp mình với ạ, mai mình thi rồi !!!!![]()
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
cho a+b+c = a^2 +b^2+c^2 =1 và x:y:z =a:b:c
CMR : (x+y+z) ^2=x^2 +y^2+z^2
Kb: Có lẽ tôi viết đến đây cũng đã nói hết cảm xúc trong lòng mình. Mọi chuyện rồi cũng sẽ ổn thôi. Đối với đây là 1 cuộc chia tay vô cùng ý nghĩa-Cuộc chia tay của những con búp bê
Đúng 0
Bình luận (0)
Ta có BĐT Bu-nhi-a-cốp-xki sau đây :
(a^2 + b^2 + c^2)(x^2 + y^2 + z^2) >= (ax + by + cz)^2
(Bạn tự cm BĐT này)
Từ đó suy ra : (a + b + c)^2 = (a.căn x / căn x + b.căn y/ căn y + c.căn z/căn z)^2
<= [(a/căn x)^2 + (b/căn y)^2 + (c/căn z)^2][(căn x)^2 + (căn y)^2 + (căn z)^2] = (a^2/x + b^2/y + c^2/z)(x+y+z)
=> a^2/x + b^2/y + c^2/z >= (a+b+c)^2/(x+y+z)
Đúng 0
Bình luận (0)