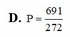Cho B = 52 + 51 + 52 + ..........+ 52016
Cho Q=52017: 4
B-Q
TN
Những câu hỏi liên quan
Bài Toàn 16 : Tính tổng
a) S 1 + 2 + 22 + 23 + … + 22017
b) S 3 + 32 + 33 + ….+ 32017
c) S 4 + 42 + 43 + … + 42017
d) S 5 + 52 + 53 + … + 52017
Đọc tiếp
Bài Toàn 16 : Tính tổng
a) S = 1 + 2 + 22 + 23 + … + 22017
b) S = 3 + 32 + 33 + ….+ 32017
c) S = 4 + 42 + 43 + … + 42017
d) S = 5 + 52 + 53 + … + 52017
a.
$S=1+2+2^2+2^3+...+2^{2017}$
$2S=2+2^2+2^3+2^4+...+2^{2018}$
$\Rightarrow 2S-S=(2+2^2+2^3+2^4+...+2^{2018}) - (1+2+2^2+2^3+...+2^{2017})$
$\Rightarrow S=2^{2018}-1$
b.
$S=3+3^2+3^3+...+3^{2017}$
$3S=3^2+3^3+3^4+...+3^{2018}$
$\Rightarrow 3S-S=(3^2+3^3+3^4+...+3^{2018})-(3+3^2+3^3+...+3^{2017})$
$\Rightarrow 2S=3^{2018}-3$
$\Rightarrow S=\frac{3^{2018}-3}{2}$
Đúng 1
Bình luận (0)
Câu c, d bạn làm tương tự a,b.
c. Nhân S với 4. Kết quả: $S=\frac{4^{2018}-4}{3}$
d. Nhân S với 5. Kết quả: $S=\frac{5^{2018}-5}{4}$
Đúng 1
Bình luận (0)
\(50-\frac{50}{51}-\frac{51}{52}-\frac{52}{53}-\frac{53}{54}-.................-\frac{99}{100}\)
So sánh : A = \(\frac{2019^{50}+1}{2020^{51}+1}\)và B = \(\frac{2019^{51}+1}{2020^{52}+1}\)
mình nhầm , thay 2019 = 2020 nhé
Tính: \(B=\frac{100^2+1^2}{100\cdot1}+\frac{99^2+2^2}{99\cdot2}+\frac{98^2+3^2}{98\cdot3}+...+\frac{52^2+49^2}{52\cdot49}+\frac{51^2+50^2}{51\cdot50}\)
Tính giá trị của x biết:
\(\frac{x-7}{50}\)+ \(\frac{x-6}{51}\)+ \(\frac{x-5}{52}\)= \(\frac{x-52}{5}\)+\(\frac{x-51}{6}\)+ \(\frac{x-50}{7}\).
mk lam luon nhe!
Bot vao moi ve 3 don vi, ta co
\(\left(\frac{x-7}{50}-1\right)+\left(\frac{x-6}{51}-1\right)+\left(\frac{x-5}{52}-1\right)=\left(\frac{x-52}{5}-1\right)+\left(\frac{x-51}{6}-1\right)+\left(\frac{x-50}{7}-1\right)\)
Quy dong len ,ta co
\(\frac{x-57}{50}+\frac{x-57}{51}+\frac{x-57}{52}=\frac{x-57}{5}+\frac{x-57}{6}+\frac{x-57}{7}\)
\(\frac{x-57}{50}+\frac{x-57}{51}+\frac{x-57}{52}-\frac{x-57}{5}-\frac{x-57}{6}-\frac{x-57}{7}=0\)
(x-57).\(\left(\frac{1}{50}+\frac{1}{51}+\frac{1}{52}-\frac{1}{5}-\frac{1}{6}-\frac{1}{7}\right)=0\)
Ma \(\left(\frac{1}{50}+\frac{1}{51}+\frac{1}{52}-\frac{1}{5}-\frac{1}{6}-\frac{1}{7}\right)\) khac 0 nen => x-57=0
x=0+57 =57
Vay x =57.
Mk chac chan 100% bai nay dung
Đúng 0
Bình luận (0)
Chứng minh rằng \(7^{50}+7^{51}-7^{52}\) chia hết cho 55
Sửa đề: \(7^{52}+7^{51}-7^{50}\)
\(=7^{50}\left(7^2+7-1\right)=7^{50}\cdot55⋮55\)
Đúng 0
Bình luận (0)
So sánh \(45^{50}+49^{51}va49^{51}+49^{52}\)
Ai nhanh mình tick cho mình cảm ơn
Ta thấy 50 + 51<51 + 52
Suy ra ; 45^50+49^51<49^51+ 49^52
Đúng 0
Bình luận (0)
\(choA=\frac{1}{1\cdot2}+\frac{1}{3\cdot4}+\frac{1}{5\cdot6}+...+\frac{1}{99\cdot100};B=\frac{1}{51\cdot100}+\frac{1}{52\cdot99}+...+\frac{1}{52\cdot99}+\frac{1}{100\cdot51}\)
\(CMR:\) \(1-\frac{1}{2}+\frac{1}{3}-...+\frac{1}{99}-\frac{1}{100}=\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\)\(=\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\)
Biến đổi vp của đẳng thức :
\(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\)
\(=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}+\frac{1}{100}-1-\frac{1}{2}-\frac{1}{3}-...-\frac{1}{50}\)
\(=1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{99}+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}-2\left[\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right]\)
\(=1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{99}-\frac{1}{2}-\frac{1}{4}-...-\frac{1}{200}\)
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
+
5
2
-
2
i
z
+
3
2
+
2
i
Biết biểu thức
Q
z
-...
Đọc tiếp
Cho số phức z thỏa mãn z + 5 2 - 2 i = z + 3 2 + 2 i Biết biểu thức Q = z - 2 - 4 i + z - 4 - 6 i đặt giá trị nhỏ nhất tại z = a + b i a , b ∈ R Tính P = a - 4b
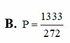
