mng giải hẳn ra hộ mik ạ. mik cảm ơn
MN
Những câu hỏi liên quan
mng giải hẳn ra giúp mik ạ. mik cảm ơn
Đọc tiếp
mng giải hẳn ra giúp mik ạ. mik cảm ơn
Lời giải:
Theo đề ta có:
\(\text{sđc(AD)}=\frac{1}{3}\text{sđc(AB)}=\frac{1}{9}[\text{sđc(AB)+sđc(BC)+sđc(CD)}]\)
\(=\frac{1}{9}(360^0-\text{sđc(AD)})\)
\(\Rightarrow \text{sđc(AD)}=36^0\)
\(\widehat{BEC}=\frac{\text{sđc(BC)-sđc(AD)}}{2}=\frac{3\text{sđc(AD)}-\text{sđc(AD)}}{2}=\text{sđc(AD)}=36^0\)
Đúng 1
Bình luận (0)
Giải hẳn ra hộ mik với ạ (đừng làm tắt), mik cảm ơn
Đọc tiếp
Giải hẳn ra hộ mik với ạ (đừng làm tắt), mik cảm ơn
ĐKXĐ: \(\left\{{}\begin{matrix}-3x\ge0\\x^2-1\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le0\\x^2\ne1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le0\\x\ne\pm1\end{matrix}\right.\)
Đúng 1
Bình luận (0)

mng giải hẳn ra hộ mik nha :3
Gọi \(J=CE\cap AB\), \(F=BD\cap AC\) , \(H=CE\cap BD\)
Có \(\widehat{EAB}=\widehat{ECB}=\dfrac{1}{2}sđ\stackrel\frown{EB}\)
\(\widehat{CAD}=\widehat{DBC}=\dfrac{1}{2}sđ\stackrel\frown{DC}\)
\(\Rightarrow\widehat{EAB}+\widehat{CAD}=\widehat{ECB}+\widehat{DBC}=180^0-\widehat{BHC}\) (*)
Lại có \(\widehat{AJC}+\widehat{AFB}=180^0\) => Tứ giác AJHF nội tiếp đường tròn
\(\Rightarrow180^0=\widehat{BAC}+\widehat{JHF}=\widehat{BAC}+\widehat{BHC}\)
\(\Rightarrow180^0-\widehat{BHC}=\widehat{BAC}\) (2*)
Từ (*); (2*) => \(\widehat{EAB}+\widehat{CAD}=\widehat{BAC}\)
\(\Leftrightarrow\widehat{EAB}+\widehat{BAC}+\widehat{CAD}=2\widehat{BAC}\)
\(\Leftrightarrow\widehat{EAD}=2\alpha\)
Ý C
Đúng 1
Bình luận (0)
mng giải hẳn ra giúp mik ạ
Đọc tiếp
mng giải hẳn ra giúp mik ạ
Lời giải:
HPT \(\Leftrightarrow \left\{\begin{matrix} xy+4x-5y-20=xy+x-4y-4\\ xy-3x+y-3=xy-2x-y+2\end{matrix}\right.\)
\( \Leftrightarrow \left\{\begin{matrix} 3x-y=16\\ -x+2y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{37}{5}\\ y=\frac{31}{5}\end{matrix}\right.\)
Khi đó: \(m+2n=\frac{37}{5}+2.\frac{31}{5}=\frac{99}{5}\)
Đúng 1
Bình luận (0)


mng giải hẳn ra giúp mik ạ ^^
Do AB bằng cạnh lục giác đều nội tiếp \(\Rightarrow\widehat{AOB}=\dfrac{1}{6}.360^0=60^0\)
\(\Rightarrow\Delta ABC\) đều \(\Rightarrow\left\{{}\begin{matrix}AB=OA=R\\OH=\dfrac{AB\sqrt{3}}{2}=\dfrac{R\sqrt{3}}{2}\end{matrix}\right.\)
Dây CD bằng cạnh tam giác đều nội tiếp \(\Rightarrow\widehat{COD}=\dfrac{1}{3}.360^0=120^0\Rightarrow\widehat{COK}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}CD=2CK=2OC.sin\widehat{COK}=R\sqrt{3}\\OK=OC.cos\widehat{COK}=\dfrac{R}{2}\end{matrix}\right.\)
\(\Rightarrow HK=OH-OK=\dfrac{R}{2}\left(\sqrt{3}-1\right)\)
\(S=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{R^2}{2}\) (chắc có sự nhầm lẫn trong đáp án, không có hằng số \(\pi\) nào ở đây)
Đúng 2
Bình luận (0)
Mik cần gấp trong tối nay ạ, trình bày hẳn ra hộ mình (không làm tắt ạ). Cảm ơn trước.
Đọc tiếp
Mik cần gấp trong tối nay ạ, trình bày hẳn ra hộ mình (không làm tắt ạ). Cảm ơn trước.
\(\sqrt{2x+5}\) xác định khi \(2x+5\ge0\Rightarrow2x\ge-5\Rightarrow x\ge-\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
\(\sqrt{2x+5}\le0\Leftrightarrow2x+5\le0\Leftrightarrow2x\le-5\Leftrightarrow x\ge\dfrac{-5}{2}\)
\(\Rightarrow\) Đáp án: A
Đúng 1
Bình luận (0)
Mik cần gấp trong tối nay ạ, trình bày hẳn ra hộ mình (không làm tắt ạ). Cảm ơn trước.
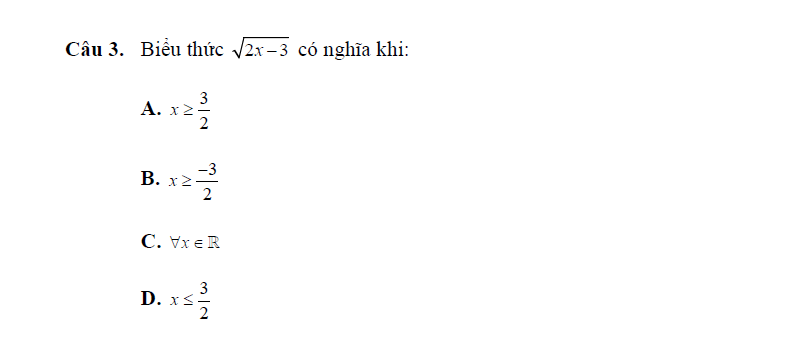
ĐKXĐ: \(2x-3\ge0\\ \Rightarrow2x\ge0+3\\ \Rightarrow2x\ge3\\ \Rightarrow x\ge\dfrac{3}{2}\left(A\right)\)
Đúng 3
Bình luận (0)
Mik cần gấp trong tối nay ạ, trình bày hẳn ra hộ mình (không làm tắt ạ). Cảm ơn trước.
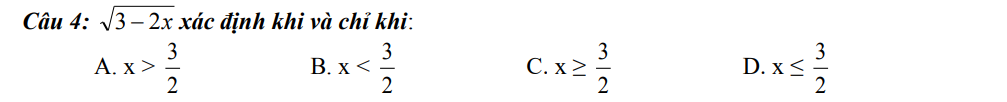
\(\sqrt{3-2x}\) xác định khi \(3-2x\ge0\Rightarrow2x\le3-0\Rightarrow2x\le3\Rightarrow x\le\dfrac{3}{2}\left(D\right)\)
Đúng 1
Bình luận (0)
\(\sqrt{3-2x}\) xác định khi: \(3-2x\ge0\)
Ta giải BPT:
\(3-2x\ge0\)
<=> \(-2x\ge-3\)
<=> \(-2x:\left(-2\right)\le-3:\left(-2\right)\)
<=> \(x\le\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
mng oi giải hộ mik câu này với,mik sắp thi rùi giải hụ mik vứi ạ mik cảm ơn 1)xác định cn,vn,tr
bạc phơ mái tóc người cha
minh ơi,bây giờ,ngoài đông,người ta đã trảy lá kè rồi





