Câu 20
KA
Những câu hỏi liên quan
Từ câu 18 đến câu 20(giải chi tiết, rồi chọn đáp án).
18.
\(-x^2+2x-5\le0\) có \(\left\{{}\begin{matrix}a=-1< 0\\\Delta'=1-5=-4< 0\end{matrix}\right.\)
\(\Rightarrow-x^2+2x-5\le0\) ; \(\forall x\in R\)
19.
Thay tọa độ lần lượt các đáp án lên thì chỉ D đúng
20.
Chu vi đường tròn: \(2\pi R=40\pi\left(cm\right)\)
Số đo của cung: \(\dfrac{35.2\pi}{40\pi}=\dfrac{7}{4}\)
Đúng 1
Bình luận (0)
Một đề thi môn Toán có 50 câu hỏi trắc nghiệm khách quan, mỗi câu có 4 phương án trả lời, trong đó có đúng một phương án là đáp án. Học sinh chọn đúng đáp án được 0,2 điểm, chọn sai đáp án không được điểm. Một học sinh làm đề thi đó, chọn ngẫu nhiên các phương án trả lời của tất cả 50 câu hỏi, xác suất để học sinh đó được 5,0 điểm bằng: A.
1
2
B.
A
50
25...
Đọc tiếp
Một đề thi môn Toán có 50 câu hỏi trắc nghiệm khách quan, mỗi câu có 4 phương án trả lời, trong đó có đúng một phương án là đáp án. Học sinh chọn đúng đáp án được 0,2 điểm, chọn sai đáp án không được điểm. Một học sinh làm đề thi đó, chọn ngẫu nhiên các phương án trả lời của tất cả 50 câu hỏi, xác suất để học sinh đó được 5,0 điểm bằng:
A. 1 2
B. A 50 25 . ( A 3 1 ) 25 ( A 4 1 ) 50
C. 1 16
D. C 50 25 . ( C 3 1 ) 25 ( C 4 1 ) 50
Một đề thi môn Toán có 50 câu hỏi trắc nghiệm khách quan, mỗi câu hỏi có 4 phương án trả lời, trong đó có đúng một phương án là đáp án. Học sinh chọn đúng đáp án được 0,2 điểm, chọn sai đáp án không được điểm. Một học sinh làm đề thi đó, chọn ngẫu nhiên các phương án trả lời của tất cả 50 câu hỏi, xác suất để học sinh đó được 5,0 điểm bằng A.
1
2
B.
A
50
25...
Đọc tiếp
Một đề thi môn Toán có 50 câu hỏi trắc nghiệm khách quan, mỗi câu hỏi có 4 phương án trả lời, trong đó có đúng một phương án là đáp án. Học sinh chọn đúng đáp án được 0,2 điểm, chọn sai đáp án không được điểm. Một học sinh làm đề thi đó, chọn ngẫu nhiên các phương án trả lời của tất cả 50 câu hỏi, xác suất để học sinh đó được 5,0 điểm bằng
A. 1 2
B. A 50 25 . A 3 1 25 A 4 1 50
C. 1 16
D. C 50 25 . C 3 1 25 C 4 1 50
Chọn đáp án D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố học sinh chỉ chọn đúng đáp án của 25 câu hỏi
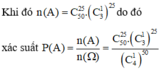
Đúng 0
Bình luận (0)
: Một đề thi trắc nghiệm môn Toán gồm 20 câu hỏi, mỗi câu hỏi có 4 phương án trả lời và chỉ có 1 phương án đúng. Mỗi câu trả lời đúng được 5 điểm, sai bị trừ 2 điểm. Do không học bài nên bạn A làm bài thi bằng cách chọn ngẫu nhiên đáp án cả 20 câu hỏi. Xác suất để bạn A đạt điểm thuộc khoảng (0;5) xấp xỉ bằng:
Một đề trắc nghiệm gồm 20 câu, mỗi câu có 4 đáp án và chỉ có một đáp án đúng. Bạn Anh làm đúng 12 câu, còn 8 câu bạn Anh đánh hú họa vào đáp án mà Anh cho là đúng. Mỗi câu đúng được 0,5 điểm. Tính xác suất để Anh được 9 điểm ? A.
63
16384
.
B.
9
10
.
C.
9
65536...
Đọc tiếp
Một đề trắc nghiệm gồm 20 câu, mỗi câu có 4 đáp án và chỉ có một đáp án đúng. Bạn Anh làm đúng 12 câu, còn 8 câu bạn Anh đánh hú họa vào đáp án mà Anh cho là đúng. Mỗi câu đúng được 0,5 điểm. Tính xác suất để Anh được 9 điểm ?
A. 63 16384 .
B. 9 10 .
C. 9 65536 .
D. 9 20 .
Đáp án A
Xác suất để Anh được điểm bằng xác suất Anh trả lời đúng câu trong câu còn lại bằng
![]()
Đúng 0
Bình luận (0)
Một đề trắc nghiệm gồm 20 câu, mỗi câu có 4 đáp án và chỉ có một đáp án đúng. Bạn Anh làm đúng 12 câu, còn 8 câu bạn Anh đánh hú họa vào đáp án mà Anh cho là đúng. Mỗi câu đúng được 0,5 điểm. Tính xác suất để Anh được 9 điểm ? A. 63/16384 B. 9/10 C. 9/65536 D. 9/20
Đọc tiếp
Một đề trắc nghiệm gồm 20 câu, mỗi câu có 4 đáp án và chỉ có một đáp án đúng. Bạn Anh làm đúng 12 câu, còn 8 câu bạn Anh đánh hú họa vào đáp án mà Anh cho là đúng. Mỗi câu đúng được 0,5 điểm. Tính xác suất để Anh được 9 điểm ?
A. 63/16384
B. 9/10
C. 9/65536
D. 9/20
Trong 8 câu còn lại, xác suất trả lời đúng mỗi câu là 1/4; xác suất trả lời sai mỗi câu là 3/4.
Xác suất để Anh được 9 điểm bằng xác suất Anh trả lời đúng 6 câu trong 8 câu còn lại bằng C 8 6 1 4 6 3 4 2 = 63 16384 .
Đáp án A
Đúng 1
Bình luận (0)
Một bài trắc nghiệm có 10 câu hỏi ,mỗi câu có 4 phương án lựa chọn trong đó có một đáp án đúng . Giả sử mỗi câu trả lời đúng được 5 điểm sai bị trừ 2 điểm . Một học sinh không học bài nên chọn ngẫu nhiên một phương án . Tính xác xuất để học sinh nhận điểm dưới 1
Giả sử học sinh đó chọn x câu đúng (với \(0\le x\le10\)), như vậy sẽ có \(10-x\) câu sai
Số điểm học sinh đó đạt được là:
\(5x-2\left(10-x\right)=7x-20\)
Điểm dưới 1 \(\Rightarrow7x-20< 1\Rightarrow x< 3\)
Vậy học sinh đó trả lời đúng 0,1 hoặc 2 câu
Xác suất đúng khi chọn mỗi câu hỏi là 1/4 còn xác suất sai là 3/4 nên xác suất học sinh đó dưới 1 điểm là:
\(C_{10}^0.\left(\dfrac{1}{4}\right)^0.\left(\dfrac{3}{4}\right)^{10-0}+C_{10}^1.\left(\dfrac{1}{4}\right)^1.\left(\dfrac{3}{4}\right)^{10-1}+C_{10}^2.\left(\dfrac{1}{4}\right)^2.\left(\dfrac{3}{4}\right)^{10-2}=...\)
Đúng 3
Bình luận (1)
cho mình hỏi câu 47 sao chọn đáp án D ạ
( cô chỉ đọc đáp án chứ không giải)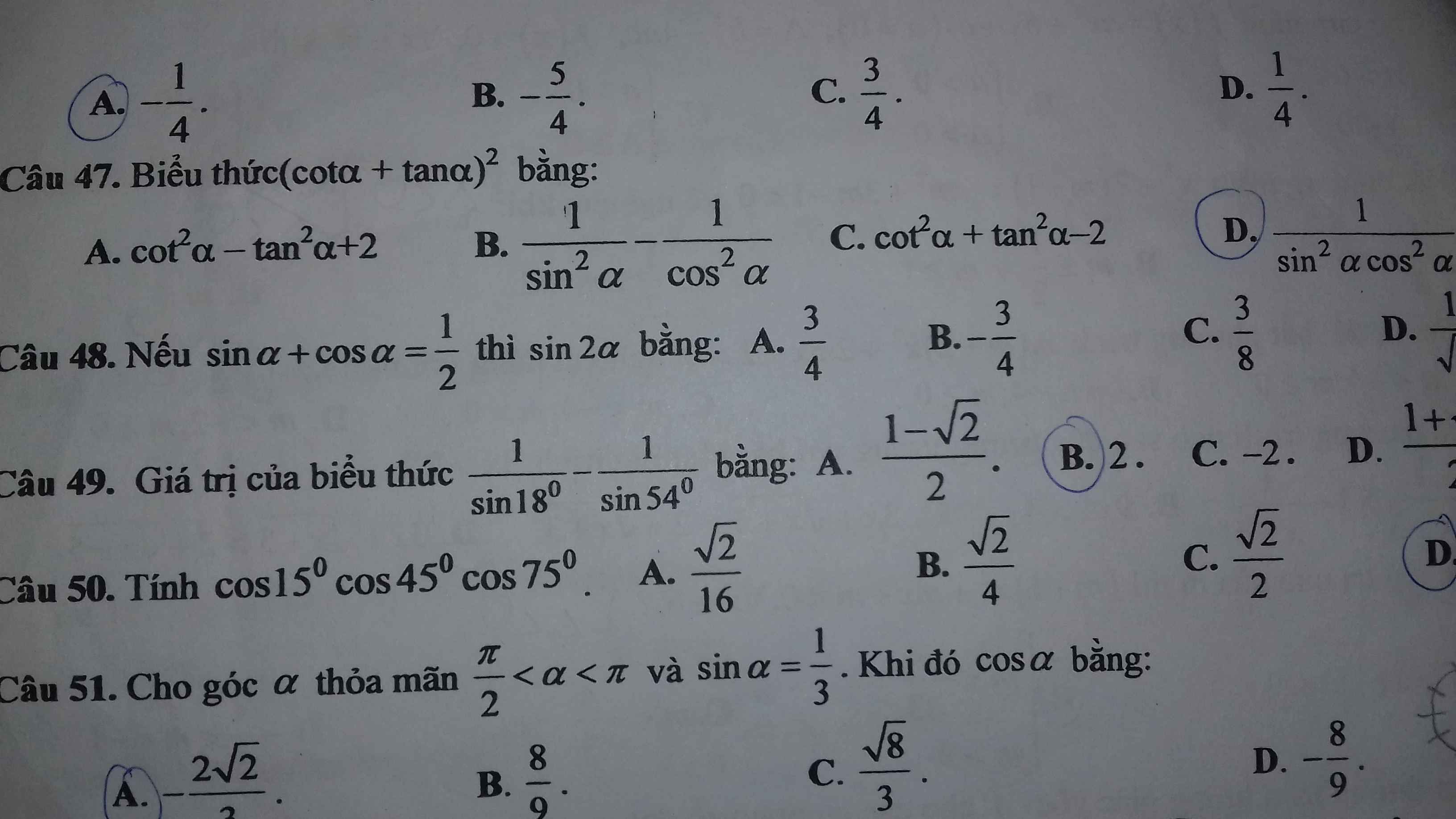
47.
\(\left(cot\alpha+tan\alpha\right)^2=\left(\dfrac{cos\alpha}{sin\alpha}+\dfrac{sin\alpha}{cos\alpha}\right)^2=\left(\dfrac{cos^2\alpha+sin^2\alpha}{sin\alpha.cos\alpha}\right)^2=\dfrac{1}{sin^2\alpha.cos^2\alpha}\)
Đúng 1
Bình luận (0)
(cota +tana)\(^2\)=cot\(^2\)a+2cota.tana+tan\(^2\)a=(cot\(^2\)a +1)+(tan\(^2\)+1)=\(\dfrac{1}{sin^2a}\)+\(\dfrac{1}{cos^2a}\)=\(\dfrac{cos^2a+sin^2a}{cos^2a.sin^2a}\)=\(\dfrac{1}{cos^2a.sin^2a}\)
Đúng 0
Bình luận (0)
\((\cot\alpha+\tan\alpha)\)2 \(=\dfrac{\cos^2\alpha}{\sin^2\alpha}+\dfrac{\sin^2\alpha}{\cos^2\alpha}+2\dfrac{\cos}{\sin}\dfrac{\sin}{\cos}\)\(=\dfrac{\cos^4\alpha+\sin^4\alpha}{\sin^2\alpha.\cos^2\alpha}+2\)\(=\dfrac{\cos^4\alpha+\sin^4\alpha+2\sin^2\alpha.\cos^2\alpha}{\sin^2\alpha.\cos^2\alpha}\)\(=\dfrac{(\cos^2\alpha+\sin^2\alpha)^2}{\sin^2\alpha.\cos^2\alpha}\)
mà : \(\sin^2+\cos^2=1\)
\(\Rightarrow\)\((\cot\alpha+\tan\alpha)\)2\(=\)\(\dfrac{1}{\sin^2\alpha.\cos^2\alpha}\)
\(\Rightarrow\)Đáp án: D
Đúng 0
Bình luận (0)
Câu 6: Từ "rập rờn" trong bài thơ trên là từ gì? Chọn đáp án đúng nhất trong các đáp án sau: *
câu 3 chọn nhiều đáp án



3,Rừng thưa, Xa van
6,Đồng bằng duyên hải
7,Khô hạn ![]()
Đúng 1
Bình luận (0)




