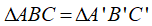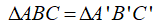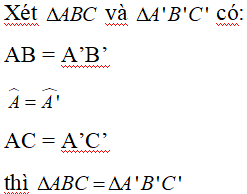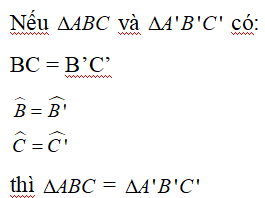
 giúp mình làm mình cảm ơn mọi người rất nhiều! Cậu nhớ ghi công thức cho mình nha mình cảm ơn 🥰
giúp mình làm mình cảm ơn mọi người rất nhiều! Cậu nhớ ghi công thức cho mình nha mình cảm ơn 🥰

Những câu hỏi liên quan
Mình đang cần gấp😱, nhờ mọi người giúp mình với ạ. Cảm ơn mọi người nhiều!!!🥰🥰🥰


Mọi người làm giúp mình bài 1,2 nha. Mình cảm ơn mn người rất nhiều
1. Định nghĩa hai tam giác bằng nhau
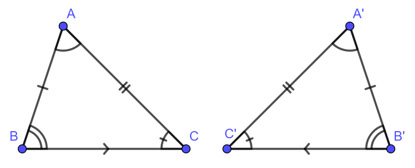
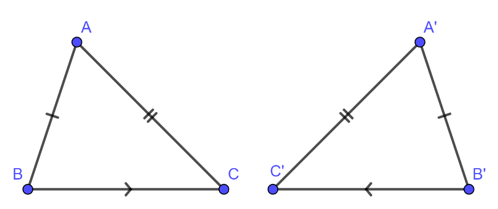
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
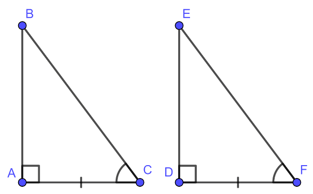
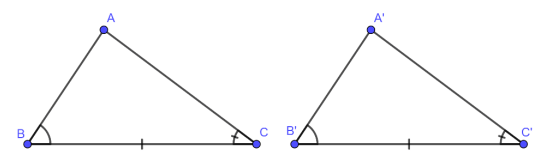
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác vuông
• Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )
• Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )
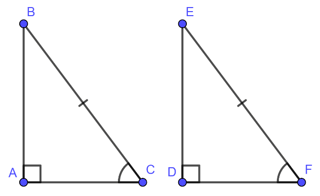
• Cạnh huyền – góc nhọn
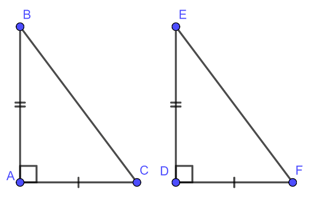
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)
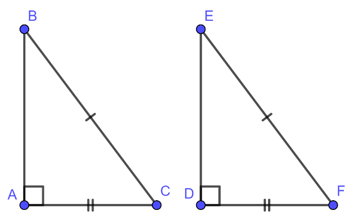
• Cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác
a. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Xét 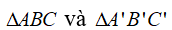
AB = A’B’
AC = A’C’
BC = B’C’
thì
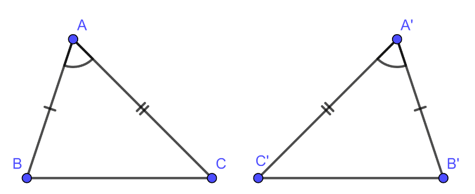
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau
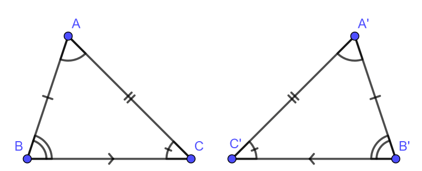
c. Trường hợp bằng nhau thứ ba của hai tam giác: góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
tik cho mình nha mình đc câu1 nè
Đúng 1
Bình luận (0)
Nếu có 20 người thì làm xong một công việc trong 7 ngày . Hỏi muốn làm xong công việc đó trong 10 ngày thì cần bao nhiêu người ? (Mức làm việc của mỗi người như nhau)
Ai trả lời câu hỏi này nhanh nhất mình rất cảm ơn và mình sẽ tick cho nè!!!
Và nhớ là phải ghi lời giải ra cho rõ ràng giùm mình nha !!!
Cảm ơn rất nhiều
mot nguoi : 20x7=140 (ngày)
10 nguoi : 140:10=14 (người)
đáp số : 14 người
1 kick nha
Đúng 0
Bình luận (0)
7 ngày gấp 10 ngày số là là :
\(7\div10=0.7\)( lần )
muốn làm công việc đó trong 10 ngày thì cần số công nhân là :
\(0.7\times20=14\)( người )
Đáp số : ..............
Đúng 0
Bình luận (0)
Số người làm xong công việc trong 10 ngày là:
20x7:10=14(người)
Đáp số:14 người
Lưu ý:dấu''x''là dấu nhân,dấu'':''là dấu chia
Thế đấy,chúc bạn học tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho mình hỏi về cách đặt câu với loại câu điều kiện (if clauses). Mọi người giúp mình ghi công thức đặt câu và ví dụ giúp mình nha♡. Cảm ơn mọi người nhiều ạh~♡
Điều kiện loại 1 :
If + S + V(s,es), S + Will/Can/shall…… + V
- Ví dụ: If the weather is nice, I will go swimming tomorrow.
Đúng 0
Bình luận (0)
#)Trả lời :
Công thức các câu điều kiện :
- Câu điều kiện loại 1 : [ If + thì hiện tại đơn ] , [ will + động từ nguyên mẫu ]
- Câu điều kiện loại 2 : [ If + thì quá khứ đơn ] , [ would + động từ nguyên mẫu ]
- Câu điều kiện loại 3 : [ If + thì quá khứ hoàn thành ] , [ would + V3 + Ved ]
#~Will~be~Pens~#
Đúng 0
Bình luận (0)
Câu điều kiện loại 2: [If + thì quá khứ đơn], [would + động từ nguyên mẫu]Ví dụ : If she knew that, she would be very surprised.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mn ơi giúp mình vs được ko ạ mình phải nộp gấp r !!! Cảm ơn mn rất nhiều 🥰🥰🥰
Mình sẽ tặng coin cho người làm đầu tiên nha
Đúng 0
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)
Đúng 1
Bình luận (0)
d: Xét ΔCBD có
CA là đường cao ứng với cạnh DB
BK là đường cao ứng với cạnh CD
CA cắt BK tại F
Do đó: F là trực tâm của ΔCBD(Tính chất ba đường cao của tam giác)
Suy ra: DF\(\perp\)BC
Ta có: DF\(\perp\)BC(cmt)
AH\(\perp\)BC(gt)
Do đó: DF//AH(Định lí 1 từ vuông góc tới song song)
Xét ΔFAB vuông tại A và ΔFAD vuông tại A có
FA chung
AB=AD
Do đó: ΔFAB=ΔFAD
Suy ra: FB=FD(hai cạnh tương ứng
Xét ΔFBD có FB=FD
nên ΔFBD cân tại F
e: Xét ΔFBD có
A là trung điểm của BD
AE//DF
Do đó: E là trung điểm của BF
Đúng 0
Bình luận (0)
 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mình trước đến giờ rất ham chơi và đã làm cho anh chị mình buồn vì rất nhiều và lực học của mình đã kém đi rất nhiều chỉ vì ham chơi mình muốn thay đổi bản thân để cho anh chị mình được tự hào vì mình và mình cần mọi người giúp đỡMình cần 1 thời gian biểu mọi người có thể giúp na được không cảm ơn các cậu trước nha!!!
Đọc tiếp
Mình trước đến giờ rất ham chơi và đã làm cho anh chị mình buồn vì rất nhiều và lực học của mình đã kém đi rất nhiều chỉ vì ham chơi mình muốn thay đổi bản thân để cho anh chị mình được tự hào vì mình và mình cần mọi người giúp đỡ
Mình cần 1 thời gian biểu mọi người có thể giúp na được không cảm ơn các cậu trước nha!!!![]()
 Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều![]()
Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$
Đúng 1
Bình luận (0)
Bài 5:a)
Xét tam giác vuông $AHB$ và $AHC$ có:
$AB=AC$ (do $ABC$ là tam giác cân ở A)
$\widehat{ABH}=\widehat{ACH}$ (do tam giác $ABC$ cân ở A)
$\Rightarrow \triangle AHB=\triangle AHC$ (cạnh huyền- góc nhọn)
$\Rightarrow HB=HC$ và $\widehat{BAH}=\widehat{CAH}$ (đpcm)
b)
$HB=HC$ nên $H$ là trung điểm $BC$. Do đó $HB=BC:2=4$ (cm)
Áp dụng định lý Pitago:
$AH=\sqrt{AB^2-AH^2}=\sqrt{5^2-4^2}=3$ (cm)
c)
Xét tam giác vuông $ADH$ và $AEH$ có:
$AH$ chung
$\widehat{DAH}=\widehat{EAH}$ (do $\widehat{BAH}=\widehat{CAH}$)
$\Rightarrow \triangle ADH=\triangle AEH$ (cạnh huyền- góc nhọn)
$\Rightarrow DH=EH$ nên tam giác $HDE$ cân tại $H$.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Có bạn nào biết làm thì giúp mình nha mình đanng cần gấp 11 giờ mình phải nộp cho thầy rồi nếu được thì mình cảm ơn nhiều, thầy này kho tính lắm.Nếu được thì mình cảm ơn rất rất nhiều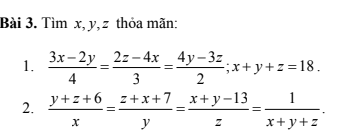
Đây là bài bạn phải nộp cho thầy nên mình sẽ không làm chi tiết. Nhưng mình có thể gợi ý cho bạn như sau:
1.
Đối với tỉ lệ thức đã cho, mỗi phân số ta nhân cả tử và mẫu với 4, 3, 2. Khi đó, ta thu được 1 tỉ lệ thức mới
Dùng tỉ lệ thức trên, áp dụng tính chất dãy tỉ số bằng nhau (cộng), ta thu được $12x=8y=6z(*)$
Tiếp tục áp dụng tính chất dãy tỉ số bằng nhau cho $(*)$ dựa theo điều kiện $x+y+z=18$ ta sẽ tính được $x,y,z$ thỏa mãn.
Đúng 0
Bình luận (0)
2.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng) cho 3 phân số đầu tiên, ta sẽ tìm được tổng $x+y+z$
Khi tìm được tổng $x+y+z$, cộng vào 3 phân số đầu tiên trong bài, mỗi phân số cộng thêm 1. Khi đó, ta thu được tỉ lệ thức $\frac{m}{x}=\frac{n}{y}=\frac{p}{z}(*)$ với $m,n,p$ đã tính được dựa theo giá trị $x+y+z$.
Áp dụng tính chất dãy tỉ số bằng nhau cho tỉ lệ thức $(*)$, kết hợp với kết quả $x+y+z$ thì bài toán đã rất quen thuộc rồi.
Đúng 0
Bình luận (0)
b)áp dụng tính chất dãy tỉ số = nhau ta có:
y+z+6+z+x+7+x+y-13/x+y+z
=2(x+y+z)/x+y+z=2
=>x+y+z=0,5
thay vào bài ta được:
0,5-x+6/x=0,5-y+7/y=0,5-z-13=2
6,5-x/x=7,5-y/y=-12,5-z/z=2
x,y,z tự tính
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi giúp mình làm từ bài 44 đến 50 với nha mọi người mình cảm ơn nhiều
4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
Đúng 3
Bình luận (1)
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
47. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{\left(a+b\right)^2}{c}+\dfrac{\left(b+c\right)^2}{a}+\dfrac{\left(c+a\right)^2}{b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+c}=\dfrac{\left[2\left(a+b+c\right)\right]^2}{a+b+c}=\dfrac{4\left(a+b+c\right)^2}{a+b+c}=4\left(a+b+c\right)\)(đpcm)
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
Xem thêm câu trả lời