Theo tính chất tia phân giác của góc ta có:

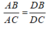
Suy ra:

Chọn đáp án D

BC=căn 3^2+4^2=5cm

AD là phân giác

=>BD/AB=CD/AC

=>BD/3=CD/4

=>BD/3=CD/4=5/7

=>BD=15/7cm; CD=20/7cm

\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

Xet ΔABC có AD là phân giác

nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7

=>BD=15/7cm; CD=20/7cm

a) Xét \(\Delta ABC:\)

AD là phân giác \(\widehat{BAC}\left(gt\right).\)

\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}\) (Tính chất phân giác).

\(\Rightarrow\dfrac{BD}{CD+BD}=\dfrac{AB}{AC+AB}.\\ \Rightarrow\dfrac{BD}{BC}=\dfrac{AB}{AC+AB}.\)

Thay: \(\dfrac{4}{BC}=\dfrac{10}{12+10}.\Rightarrow BC=8,8\left(cm\right).\)

Vậy \(BC=8,8\left(cm\right).\)

\(BC=\sqrt{3^2+4^2}=5\)

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{12}{5}cm\)

\(AD=\sqrt{bc\left(1-\left(1-\dfrac{a}{b+C}\right)^2\right)}=\dfrac{4\sqrt{3}}{7}\)

amXét \(\Delta ABC\)có AD là tia phân giác của \(\widehat{A}\)

Áp dụng tính chất của đường phân giác ,ta có:

\(\frac{DB}{DC}\)= \(\frac{AB}{AC}\)=\(\frac{4}{6}\)=\(\frac{2}{3}\)

b,theo câu a ta có :

\(\frac{DB}{DC}\)=\(\frac{2}{3}\)\(\Leftrightarrow\frac{DB}{3}\)=\(\frac{2}{3}\)

                         \(\Leftrightarrow DB=\frac{2.3}{3}\) 

                          \(\Leftrightarrow DB=2\)

Áp dụng định lí trên ta có: Δ ABC, AD là đường phân giác của góc B A C ^  ( D ∈ BC )

Ta có DB/AB = DC/AC hay 2/3 = DC /4 ⇒ DC = (2.4)/ 3 = 8/3 = 2,(6 ) ( cm )

Áp dụng định lí trên ta có: Δ ABC, AD là đường phân giác của góc  B A C ^  ( D ∈ BC )

Ta có DB/AB = DC/AC hay 2/3 = DC /4 ⇒ DC = (2.4)/ 3 = 8/3 = 2,(6 ) ( cm ) 

1: Xét tứ giác AMDN có

góc AMD=góc AND=góc MAN=90 độ

AD là phan giác

=>AMDN là hình vuông

2: BC=căn 3^2+4^2=5cm

AD là phân giác

=>DB/AB=CD/AC

=>BD/3=CD/4=(BD+CD)/(3+4)=5/7

=>BD=15/7cm; CD=20/7cm