Tìm x,y :
3xy + y - 2x + 1 =0
1)Tìm x,y thỏa mãn:
x2-3xy+2y2 = 0 và 2x2 - 3xy + 5 = 0
2) Tìm x,y thỏa mãn:
(x-y)2 + 3(x-y) = 4 và 2x + 3y = 12
x^2 + 3xy + 2y^2 = 0
=> x^2 + xy + 2xy + 2y^2 = 0
=> x(x+y) + 2y ( x+ y ) = 0 =
=> ( x+ 2y)( x + y ) = 0
=> x = -2y hoặc x = -y
(+) x = -2y thay vào ta có :
8y^2 + 6y + 5 = 0 giải ra y => x
(+) thay x = -y ta có :
2y^2 - 3y + 5 = 0 tương tự
phân tích đa thức sau thành nhân tử
1,3x^2+x-2
2, 2x^2-3xy-2y^2
3, 2x^2-3xy-2y^2
4, x^2+4xy+2x+3y^2+6
5, x^8+x+1
Tìm x,y biết
1, x^2+2x+5+y^2-4y=0
2,4x^2+y^4-20x-2y=26=0
mik ko bít
I don't now
................................
.............
1, Tìm tất cả các số nguyên x, y thỏa mãn phương trình 2x ^ 2 + y ^ 2 + 3xy - 3x - 3y + 11 = 0
Tìm giá trị biểu thức \(C=2x^6y-3xy^3-20\) với x,y thỏa mãn \(\left|x+1\right|+\left(y-2\right)^2=0\)
-Có \(\left|x+1\right|+\left(y-2\right)^2=0\)
-Vì \(\left|x+1\right|\ge0\forall x;\left(y-2\right)^2\ge0\forall y\)
\(\Rightarrow\left|x+1\right|=0\) ; \(\left(y-2\right)^2=0\)
\(\Rightarrow x=-1;y=2\)
-Thay \(x=-1;y=2\) vào \(C=2x^6y-3xy^3-20\) ta được:
\(C=2.\left(-1\right)^6.2-3.\left(-1\right).2^3-20=8\)
1/tìm các cặp số nguyên (x;y) thỏa mãn:\(5x^2+2xy+y^2-4x-40=0\)0
2/tìm các số nguyên x;y thỏa mãn:\(3xy+x+15y-44=0\)
3/gtp nghiệm nguyên :\(2x^2+3xy-2y^2=7\)
\(3xy+x+15y-44=0\)
\(3y\left(x+5\right)+\left(x+5\right)-49=0\)
\(\left(x+5\right)\left(3y+1\right)=49\)
Vì x;y là số nguyên \(\Rightarrow\hept{\begin{cases}x+5\in Z\\3y+1\in Z\end{cases}}\)
Có \(\left(x+5\right)\left(3y+1\right)=49\)
\(\Rightarrow\left(x+5\right)\left(3y+1\right)\in\text{Ư}\left(49\right)=\left\{\pm1;\pm7;\pm49\right\}\)
b tự lập bảng nhé~
tìm y va x biet 3xy+2y+2x=0
x^3+y^3=3xy-1
x^3+y^3-3xy+1=0
(x+y)^3-3xy(x+y)-3xy+1=0
(x+y+1)(x^2+2xy+y^2-x-y+1)-3xy(x+y+1)=0
(x+y+1)(x^2+2xy+y^2-x-y+1-3xy)=0
suy ra +)x+y+1=0.VÌ x,y thuộc N* nên x+y+1 khác 0
+)x^2-xy+y^2+1-x-y=0
2(x^2-xy+y^2+1-x-y)=0
2x^2-2xy+2y^2+2-2x-2y=0
(x^2-2xy+y^2)+(x^2-2x+1)+(y^2-2y+1)=0
(x-y)^2+(x-1)^2+(y-1)^2=0
suy ra +)x-y=0
+)x-1=0
+)y-1=0
Vậy x=y=1
Cho x + y = 0. Giá trị của biểu thức 1 – 3xy(x+y) + 2x 3 y + 2x 2 y 2 – 5
bài 4 tìm x;y ϵ N
a 2y*(3x-1)+9x-3=7
b 3xy-2x+3y-9=0
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: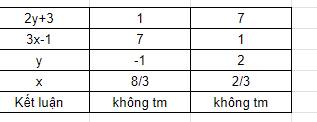
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
Tìm x, y biết:
a) (x-1)(y+2)=7
b)x(y - 1) + y = 4
c) xy - 2x + y = 4
d)x^2 - 3xy + 2x - 6y = 5
`@` `\text {Ans}`
`\downarrow`
`a)`
`(x-1)(y+2)=7`
`=> (x - 1)(y + 2) \in` Ư`(7) = {7; 1; -1; -7}`
Ta có bảng sau:
| `x - 1` | `7` | `1` | `-1` | `-7` |
| `y + 2` | `1` | `7` | `-7` | `-1` |
| `x` | `8` | `2` | `0` | `-6` |
| `y` | `-1` | `5` | `-9` | `-3` |
Vậy, ta có cặp `(x; y)` thỏa mãn `{-1; 8}; {2; 5}; {-9; 0}; {-6; -3}`
`b)`
`x(y - 1) + y = 4`
`=> x(y - 1) + y - 4 = 0`
`=> x(y - 1) + (y - 1) - 3 = 0`
`=> (x + 1)(y - 1) = 3`
`=> (x + 1)(y - 1) \in` Ư`(3) = {-1; -3; 1; 3}`
Ta có bảng sau:
| `x + 1` | `1` | `3` | `-1` | `-3` |
| `y - 1` | `3` | `1` | `-3` | `-1` |
| `x` | `0` | `2` | `-2` | `-4` |
| `y` | `4` | `2` | `-2` | `0` |
Vậy, ta có cặp `(x; y)` thỏa mãn `{0; 4}; {2; 2}; {-2; -2}; {-4; 0}`