\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)

b:

\(D=-25x^2+10x-1-10\)

\(=-\left(25x^2-10x+1\right)-10\)

\(=-\left(5x-1\right)^2-10< =-10\)

Dấu = xảy ra khi x=1/5

\(E=-9x^2-6x-1+20\)

\(=-\left(9x^2+6x+1\right)+20\)

\(=-\left(3x+1\right)^2+20< =20\)

Dấu = xảy ra khi x=-1/3

\(F=-x^2+2x-1+1\)

\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)

Dấu = xảy ra khi x=1

Biểu thức  x 2 - 25 x 2 - 10 x + 25 x xác định khi x 0 và x  ≠  5.

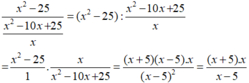
Ta có: 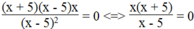khi x(x + 5) = 0 và x – 5  ≠  0

x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5

x = 0 không thỏa mãn điều kiện.

Vậy x = - 5 thì biểu thức  x 2 - 25 x 2 - 10 x + 25 x có giá trị bằng 0.

Biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5  xác định khi x ≠ 5 và x  ≠  - 5

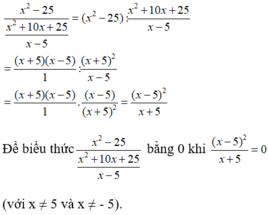
x - 5 2  = 0 ⇔ x – 5 = 0 ⇔ x= 5

x = 5 không thỏa mãn điều kiện.

Vậy không có giá trị nào của x để biểu thức  x 2 - 25 x 2 + 10 x + 25 x - 5 có giá trị bằng 0.

Biểu thức  x 2 - 25 x 2 - 10 x + 25 x xác định khi x 2 - 10 x + 25 ≠ 0 và x  ≠  0

x 2 - 10 x + 25   ≠  0 ⇔ x - 5 2   ≠  0 ⇔ x  ≠  5

Vậy điều kiện để biểu thức xác định là x  ≠  0 và x  ≠  5

Biểu thức  x 2 - 25 x 2 + 10 x + 25 x - 5 xác định khi x 2 + 10 x + 25 ≠ 0 và x - 5  ≠  0

x 2 + 10 x + 25   ≠  0 ⇔ x + 5 2   ≠  0 ⇔ x  ≠  - 5

x – 5  ≠  0 ⇔ x  ≠  5

Vậy điều kiện để biểu thức xác định là x  ≠  5 và x  ≠  - 5.

_hì^^!!

a) Ta có: \(25x^2-20x+7\)

\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)

\(=\left(5x-2\right)^2+3\ge3\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{2}{5}\)

b) Ta có: \(9x^2-6x+2\)

\(=9x^2-6x+1+1\)

\(=\left(3x-1\right)^2+1\ge1\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{3}\)

c) Ta có: \(-x^2+2x-2\)

\(=-\left(x^2-2x+2\right)\)

\(=-\left(x^2-2x+1+1\right)\)

\(=-\left(x-1\right)^2-1\le-1\forall x\)

Dấu '=' xảy ra khi x-1=0

hay x=1

d) Ta có: \(x^2+12x+39\)

\(=x^2+12x+36+3\)

\(=\left(x+6\right)^2+3\ge3\forall x\)

Dấu '=' xảy ra khi x=-6

e) Ta có: \(-x^2-12x\)

\(=-\left(x^2+12x+36-36\right)\)

\(=-\left(x+6\right)^2+36\le36\forall x\)

Dấu '=' xảy ra khi x=-6

f) Ta có: \(4x-x^2+1\)

\(=-\left(x^2-4x-1\right)\)

\(=-\left(x^2-4x+4-5\right)\)

\(=-\left(x-2\right)^2+5\le5\forall x\)

Dấu '=' xảy ra khi x=2

a) Ta có: \(25x^2-20x+7\)

\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)

\(=\left(5x-2\right)^2+3\ge3\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{2}{5}\)

b) Ta có: \(9x^2-6x+2\)

\(=9x^2-6x+1+1\)

\(=\left(3x-1\right)^2+1\ge1\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{3}\)

c) Ta có: \(-x^2+2x-2\)

\(=-\left(x^2-2x+2\right)\)

\(=-\left(x^2-2x+1+1\right)\)

\(=-\left(x-1\right)^2-1\le-1\forall x\)

Dấu '=' xảy ra khi x=1

( Mình trình bày mẫu câu a các câu khác mình làm tắt lại nhưng tương tự trình bày câu a nha )

a, Ta có : \(25x^2-20x+7=\left(5x\right)^2-2.5x.2+2^2+3\)

\(=\left(5x-2\right)^2+3\)

Thấy : \(\left(5x-2\right)^2\ge0\forall x\in R\)

\(\Rightarrow\left(5x-2\right)^2+3\ge3\forall x\in R\)

Vậy \(Min=3\Leftrightarrow5x-2=0\Leftrightarrow x=\dfrac{2}{5}\)

b, \(=9x^2-2.3x+1+1=\left(3x-1\right)^2+1\ge1\)

Vậy Min = 1 <=> x = 1/3

c, \(=-x^2+2x-1-1=-\left(x^2-2x+1\right)-1=-\left(x-1\right)^2-1\le-1\)

Vậy Max = -1 <=> x = 1

d, \(=x^2+2.x.6+36+3=\left(x+6\right)^2+3\ge3\)

Vậy Min = 3 <=> x = - 6

e, \(=-x^2-2.x.6-36+36=-\left(x+6\right)^2+36\le36\)

Vậy Max = 36 <=> x = -6 .

f, \(=-x^2+4x-4+5=-\left(x^2-4x+4\right)+5=-\left(x-2\right)^2+5\le5\)

Vậy Max = 5 <=> x = 2

\(A=x^2-10x+32=x^2-10x+25+9=\left(x-5\right)^2+9\)

mà \(\left(x-5\right)^2\ge0\)

\(\Rightarrow\left(x-5\right)^2+9\ge9\)

\(\Rightarrow Min\left(A\right)=9\)

A=x2−10x+32=x2−10x+25+9=(x−5)2+9

mà (�−5)2≥0(x−5)2≥0

⇒(�−5)2+9≥9⇒(x−5)2+9≥9

$\Rightarrow Min\left(A\right)=9$