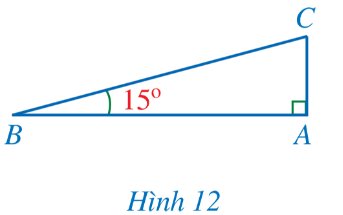
Tính độ cao AC trong Hình 12 khi BC = 20 m (làm tròn kết quả đến hàng phần mười của mét).
Trong bài toán ở phần mở đầu, độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Xem chi tiết
- Cách 1:
Hàm số biểu diễn đồ thị \(y = - 0,00188{\left( {x - 251,5} \right)^2} + 118\)
\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)
Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)
- Cách 2:
Ta có phương trình thành cầu: \(y = – 0,00188(x – 251,5)^2 + 118\)
\( \Leftrightarrow y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai.
Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I.
Ta có: \(b = 0,94564, c = – 0,91423\)
\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I = – 0,00188(x_I – 251,5)^2 + 118 =118.\)
Vậy độ cao lớn nhất cần tìm là 118 m.
Dùng máy tính cầm tay để A) tính độ dài cạnh của một miếng đất hình vuông có S=12 996m² B) Tính bán kính của 1 hình tròn có S=100 cm²(làm tròn kết quả đến hàng phần mười)
Lời giải:
a. Ta có: $12996=114\times 114$ nên độ dài cạnh miếng đất là $114$ (m)
b. $3,14 R^2=100$
$R^2=100:3,14$=31,84$
$R=\sqrt{31,84}=5,6$ (cm)
Cho tam giác ABC có \(AB = 3,5;\;AC = 7,5;\;\widehat A = {135^o}.\) Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là:92,1
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:-845,7
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là:-72,9
\(92,117\approx92,12\\ -845,654\approx-845,65\approx-845,7\\ 82,572\approx82,57\\ 82,572\approx82,57\\ -72,882\approx-72,9\)
Làm tròn số 92,117 đến hàng phần mười được kết quả là:
Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
Làm tròn số 82,572 đến hàng phần mười được kết quả :
Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
Làm tròn số -7671,08 đến hàng chục được kết quả là
Làm tròn số 86427 đến hàng trăm được kết quả là:
Làm tròn số 28,1 đến hàng đơn vị được kết quả là:
Làm tròn số -28,7 đến hàng đơn vị được kết quả là
Làm tròn số 128,5 đến hàng chục được kết quả là:
Làm tròn số 28,23 đến hàng đơn vị được kết quả là:
Làm tròn số 5960,12 đến hàng trăm được kết quả là
Làm tròn số -2367,785 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số 327,7892 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -29670 đến hàng nghìn được kết quả là:
Làm tròn số 7476,5 đến hàng đơn vị được kết quả là
Làm tròn số 4568,12 đến hàng trăm được kết quả là:
Làm tròn số -28,39 đến hàng phần mười được kết quả là:
Làm tròn số -67,193 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -18,119 đến chữ số thập phân thứ hai được kết quả là
Làm tròn số -15427,99 đến hàng trăm được kết quả là:
chu vi tam giác đều = 20 cm. tính độ dài cạch của tam giác (làm tròn đến kết quả đến hàng phần trăm)
Độ dài cạnh của tam giác là:
\(\dfrac{20}{3}\simeq6,67\left(cm\right)\)
Một bánh xe hình tròn có đường kính là 700 mm chuyển động trên một đường thẳng từ điểm A đến điểm B sau 875 vòng. Quãng đường AB dài khoảng bao nhiêu ki-lô-mét (làm tròn kết quả đến hàng phần mười và lấy π = 3,14)?
Cho tam giác ABC có \(AB = 3,AC = 4,\widehat {BAC} = {120^o}.\) Tính (làm tròn kết quả đến hàng đơn vị):
a) Độ dài cạnh BC và độ lớn góc B.
b) Bán kính đường tròn ngoại tiếp
c) Diện tích của tam giác
d) Độ dài đường cao xuất phát từ A
e) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BC} \) với M là trung điểm của BC.
a) Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {3^2} + {4^2} - 2.3.4.\cos {120^o}\\ \Leftrightarrow B{C^2} = 37\\ \Leftrightarrow BC \approx 6\end{array}\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = 2R\\ \Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{4.\sin {{120}^o}}}{6} = \frac{{\sqrt 3 }}{3}\\ \Leftrightarrow \widehat B \approx {35^o}\end{array}\)
b) \(R = \frac{{BC}}{{2.\sin A}} = \frac{6}{{2.\sin {{120}^o}}} = 2\sqrt 3 \)
c) Diện tích tam giác ABC: \(S = \frac{1}{2}4.3.\sin {120^o} = 3\sqrt 3 .\)
d) Gọi H là chân đường cao hạ từ đỉnh A.
Ta có: \(S = \frac{1}{2}AH.BC\)
\( \Rightarrow AH = \frac{{2S}}{{BC}} = \frac{{2.3\sqrt 3 }}{6} = \sqrt 3 \)
e) \(\overrightarrow {AB} .\overrightarrow {AC} = 3.4.\cos (\widehat {BAC}) = 12.\cos {120^o} = - 6.\)
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) (do M là trung điểm BC)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} .\overrightarrow {BC} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )(\overrightarrow {AC} - \overrightarrow {AB} )\\ = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right)\\ = \frac{1}{2}\left( {{4^2} - {3^2}} \right) = \frac{7}{2}.\end{array}\)
Bài 3: Để chạy xe từ sân lên nhà, người ta làm một cầu dắt xe như hình vẽ. Biết độ cao của bậc thềm AB = 55 cm, chiều dài từ chân bậc thềm tới điểm đặt còn lại của cầu dắt xe là AC = 75cm. Tính chiều dài của cầu dắt xe (kết quả làm tròn đến hàng phần mười)? (1đ)
Bài 4: Hình bên là một cái lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ:
a/ Thể tích không khí bên trong lều là bao nhiêu biết chiều cao của chiếc lều là 2,8 m và độ dài cạnh đáy của lều 4,8 m ?
b/ Xác định số vải bạt cần thiết để dựng lều ( không tính đến đường viền, nếp gấp, đáy…) là bao nhiêu ? Biết chiều cao mặt bên của lều trại là 4m
Bài : Cho tam giác ABC vuông tại A ( AB < AC). Gọi M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M lên AB và AC.
a/ Chứng minh: ADME là hình chữ nhật (1 đ)
b/ Chứng minh: D là trung điểm của AB và BMEB là hình bình hành. (1 đ)
c/ Gọi N là điểm đối xứng của M qua D, P là điểm đối xứng của M qua E. Chứng minh: P, A, N thẳng hàng (0,5 đ)
E cảm ơn nhiều ạa
Bài 3,4: Bạn cho mình xin hình vẽ nha bạn
Bài 5:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b:
Sửa đề: Chứng minh BMED là hình bình hành
Xét ΔABC có
M là trung điểm của BC
MD//AC(Cùng vuông góc với AB)
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB(cùng vuông góc với AC)
Do đó: E là trung điểm của AC
Xét ΔABC có
E,M lần lượt là trung điểm của CA,CB
=>EM là đường trung bình của ΔABC
=>EM//AB và \(EM=\dfrac{AB}{2}\)
Ta có: EM//AB
D\(\in\)AB
Do đó: EM//BD
Ta có: \(EM=\dfrac{AB}{2}\)
\(DB=\dfrac{AB}{2}\)
Do đó: EM=BD
Xét tứ giác EMBD có
EM//BD
EM=BD
Do đó: EMBD là hình bình hành
c: Xét tứ giác AMBN có
D là trung điểm chung của AB và MN
=>AMBN là hình bình hành
Hình bình hành AMBN có MN\(\perp\)AB
nên AMBN là hình bình hành
=>AB là phân giác của góc MAN
=>\(\widehat{MAN}=2\cdot\widehat{MAB}\)
Xét tứ giác AMCP có
E là trung điểm chung của AC và MP
=>AMCP là hình bình hành
Hình bình hành AMCP có AC\(\perp\)MP
nên AMCP là hình thoi
=>AC là phân giác của góc MAP
=>\(\widehat{MAP}=2\cdot\widehat{MAC}\)
Ta có: \(\widehat{MAP}+\widehat{MAN}=\widehat{PAN}\)
=>\(\widehat{PAN}=2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)\)
=>\(\widehat{PAN}=2\cdot\widehat{BAC}=180^0\)
=>P,A,N thẳng hàng
Câu 9: Chia đều 1 thanh gỗ dài 8,32m thành 4 đoạn thẳng bằng nhau. Tính độ dài mỗi đoạn gỗ ( Làm tròn kết quả đến hàng phần mười)
A.2m B.2,18m C.2,1m D.2,08m