Bài 3: Để chạy xe từ sân lên nhà, người ta làm một cầu dắt xe như hình vẽ. Biết độ cao của bậc thềm AB = 55 cm, chiều dài từ chân bậc thềm tới điểm đặt còn lại của cầu dắt xe là AC = 75cm. Tính chiều dài của cầu dắt xe (kết quả làm tròn đến hàng phần mười)? (1đ)
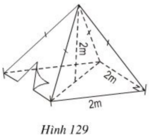
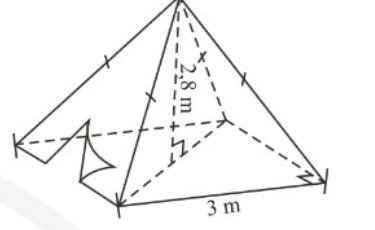
Bài 4: Hình bên là một cái lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ:
a/ Thể tích không khí bên trong lều là bao nhiêu biết chiều cao của chiếc lều là 2,8 m và độ dài cạnh đáy của lều 4,8 m ?
b/ Xác định số vải bạt cần thiết để dựng lều ( không tính đến đường viền, nếp gấp, đáy…) là bao nhiêu ? Biết chiều cao mặt bên của lều trại là 4m
Bài : Cho tam giác ABC vuông tại A ( AB < AC). Gọi M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M lên AB và AC.
a/ Chứng minh: ADME là hình chữ nhật (1 đ)
b/ Chứng minh: D là trung điểm của AB và BMEB là hình bình hành. (1 đ)
c/ Gọi N là điểm đối xứng của M qua D, P là điểm đối xứng của M qua E. Chứng minh: P, A, N thẳng hàng (0,5 đ)
E cảm ơn nhiều ạa
Bài 3,4: Bạn cho mình xin hình vẽ nha bạn
Bài 5:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b:
Sửa đề: Chứng minh BMED là hình bình hành
Xét ΔABC có
M là trung điểm của BC
MD//AC(Cùng vuông góc với AB)
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB(cùng vuông góc với AC)
Do đó: E là trung điểm của AC
Xét ΔABC có
E,M lần lượt là trung điểm của CA,CB
=>EM là đường trung bình của ΔABC
=>EM//AB và \(EM=\dfrac{AB}{2}\)
Ta có: EM//AB
D\(\in\)AB
Do đó: EM//BD
Ta có: \(EM=\dfrac{AB}{2}\)
\(DB=\dfrac{AB}{2}\)
Do đó: EM=BD
Xét tứ giác EMBD có
EM//BD
EM=BD
Do đó: EMBD là hình bình hành
c: Xét tứ giác AMBN có
D là trung điểm chung của AB và MN
=>AMBN là hình bình hành
Hình bình hành AMBN có MN\(\perp\)AB
nên AMBN là hình bình hành
=>AB là phân giác của góc MAN
=>\(\widehat{MAN}=2\cdot\widehat{MAB}\)
Xét tứ giác AMCP có
E là trung điểm chung của AC và MP
=>AMCP là hình bình hành
Hình bình hành AMCP có AC\(\perp\)MP
nên AMCP là hình thoi
=>AC là phân giác của góc MAP
=>\(\widehat{MAP}=2\cdot\widehat{MAC}\)
Ta có: \(\widehat{MAP}+\widehat{MAN}=\widehat{PAN}\)
=>\(\widehat{PAN}=2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)\)
=>\(\widehat{PAN}=2\cdot\widehat{BAC}=180^0\)
=>P,A,N thẳng hàng