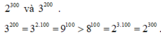so sánh 2300 và 2550
PM
Những câu hỏi liên quan
So sánh: 2 300 và 3 200
So sánh: 2300 và 3200
2300 = (23)100 = 8100 và 3200 = (32)100 = 9100 nên 2300 < 3200;
Đúng 0
Bình luận (0)
so sánh 50^20 và 2550^10
\(50^{20}=\left(50^2\right)^{10}=2500^{10}<2550^{10}\)
Đúng 0
Bình luận (0)
ta có
5020 = (502)10 = 250010
vì 2500 < 2550 nên 520 < 25501
k đúng chi mik nha
so sánh A= -15/2300 + -17/3200
B=-17/2300 + -15/3200
so sánh : 5020 và 255010
5020 = 50 x 50 x 50 x ... x 50 x 50 (có 20 số)
= (50 x 50) x (50 x 50) x ... x (50 x 50) (có 10 cặp)
= 2500 x 2500 x ... x 2500 (có 10 số)
= 250010
Mà 250010 < 255010 => 5020 < 255010
Đúng 0
Bình luận (0)
ta có:
\(50^{20}=50^{2x10}=\left(50^2\right)^{10}=2500^{10}\)
Vì \(2500< 2550=>2500^{10}< 2550^{10}=>50^{20}< 2550^{10}\)
Vậy \(50^{20}< 2550^{10}\)
Đúng 0
Bình luận (0)
\(50^{20}\)và \(2550^{10}\)
Ta có :
\(50^{20}=\left(50^2\right)^{10}=2500^{10}\)
Vì \(2500< 2550\)nên \(50^{20}< 2550^{10}\)
Đúng 0
Bình luận (0)
Bài 1: So sánh
1/ a) 2300 và 3200 b) 9920 và 999910 c) 3500 và 7300
d) 202303 và 303202 e) 10750 và 7375
a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)
c) \(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=\left(7^3\right)^{100}=343^{100}>243^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)
Đúng 3
Bình luận (0)
\(\left(d\right):202^{303}=\left(202^3\right)^{101}=8242408^{101}>303^{202}=\left(303^2\right)^{101}=91809^{101}\)
\(\left(e\right):107^{50}=\left(107^2\right)^{25}=11449^{25}< 73^{75}=\left(73^3\right)^{25}=389017^{25}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
So sánh
5020 và 255010
Ai giải nhanh và đúng mk sẽ tick
Ta có
\(2550^{10}=\left(51.50\right)^{10}=51^{10}.50^{10}>50^{10}.50^{10}=50^{20}\)
Vậy\(50^{20}< 2550^{10}\)
Đúng 0
Bình luận (0)
5020 và 255010
5020= (52)10= 2510
Ta thấy 2510 và 255010có cùng chung một số mũ nên 255010 không cần phải tính nữa.
Vậy : 5020< 255010
Đúng 0
Bình luận (0)
Ta co :
50^20=(502)10=250010
Do 250010<255010
Vay 5020<255010
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
so sánh :
a. 5020 và 255010
b. 375 và 550
a/ ta co \(50^{20}=\left(50^2\right)^{10}\)
\(\left(50^2\right)^{10}=2500^{10}< 2550^{10}\)
Hay \(50^{20}< 2550^{10}\)
b/ ta có \(3^{75}=\left(3^3\right)^{25}\)
\(5^{50}=\left(5^2\right)^{25}\)
\(\Rightarrow\left(3^3\right)^{25}=27^{25}\)
\(\Rightarrow\left(5^2\right)^{25}=25^{25}\)
Vay \(3^{75}>5^{50}\)
Đúng 0
Bình luận (0)
So sánh :
a) 5020 và 255010
b) 99910 và 9999995
a. Ta có: \(50^{20}=50^{2.10}=2500^{10}< 2550^{10}\)
Vậy \(5^{20}< 2550^{10}\)
Ý b làm tương tự, tách 10 thành 5.2 là được.
Đúng 0
Bình luận (0)
a) 5020 và 255010
ta có : 5020=(502)10=250010
=> 250010<255010
vì 2500<2550 và 10=10
hay 5020<255010
Vậy 5020<255010
b)99910 và 9999995
Ta có : 99910 = (9992)5
9999995 = (999.1001)5
Ta thấy : (9992)=999.999
999.999 < 999.1001 vì 999<1001
=> 9992<999.1001
=>(9992)5<(999.1001)5
hay 99910<9999995
Vậy 99910< 9999995
Đúng 0
Bình luận (1)
So sánh các phân số dưới đây mà không cần quy đồng:
\(\dfrac{1999}{1990}\) và \(\dfrac{2000}{1991}\)
\(\dfrac{2780}{2770}\) và \(\dfrac{2555}{2550}\)
\(\dfrac{8089}{8080}\) và \(\dfrac{9879}{9870}\)
1999/1990 và 2000/1991
1999/1990-1=9/1990
2000/1991-1=9/1991
Vì 9/1990>9/1991 nên 1999/1990 < 2000/1991
2780/2770 và 2555/2550
2780/2770 -1=1/277
2555/2550-1=1/510
Vì 1/277>1/510 nên 2780/2770 < 2555/2550
8089/8080 và 9879/9870
8089/8080-1=9/8080
9879/9870-1=3/3290=9/9870
Vì 9/8080> 9/9870 nên 8089/8080< 9879/9870
Đúng 3
Bình luận (1)