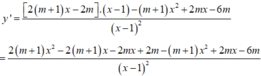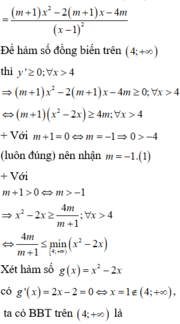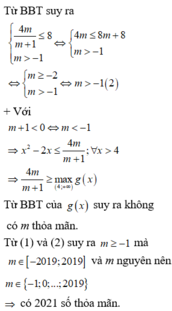Số giá trị của m để giá trị lớn nhất của hàm số \(y=x^4-6mx^2+m^2\) trên [-2;1] bằng 16 là ?
BB
Những câu hỏi liên quan
Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số y=|x^2+2x+m-4| trên đoạn [-2;-1] bằng 4
Tìm m để giá trị lớn nhất của hàm số
y
x
2
+
2
x
+
m
-
4
trên đoạn [-2; 1] đạt giá trị nhỏ nhất. Giá trị của m là A. 4 B. 3 C. 1 D. 2
Đọc tiếp
Tìm m để giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn [-2; 1] đạt giá trị nhỏ nhất. Giá trị của m là
A. 4
B. 3
C. 1
D. 2
y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5
Ta có ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1
Giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số y=(3m-4)x\(^2\) với m\(\ne\)\(\dfrac{4}{3}\). Tìm các giá trị của tham số m để hàm số :
a) Đạt giá trị lớn nhất là 0
b) Đạt giá trị nhỏ nhất là 0
a) Để m đạt giá trị lớn nhất là 0 thì \(y=\left(3m-4\right)x^2\le0\) ⇔ \(3m-4\le0\)
⇔ \(m\le\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị lớn nhất là 0 thì \(m< \dfrac{4}{3}\)
b) Để m đạt giá trị nhỏ nhất là 0 thì \(y=\left(3m-4\right)x^2\ge0\) ⇔ \(3m-4\ge0\)
⇔ \(m\ge\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị nhỏ nhất là 0 thì \(m>\dfrac{4}{3}\)
Đúng 4
Bình luận (0)
Cho hàm số y= 2x^2 -3(m+1)x +m^2 +3m -2 , m là tham số . TÌm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
Số các giá trị nguyên của tham
M
∈
-
2019
;
2019
để hàm số
y
m
+
1
2...
Đọc tiếp
Số các giá trị nguyên của tham M ∈ - 2019 ; 2019 để hàm số y = m + 1 2 - 2 m x + 6 m x - 1 đồng biến trên khoảng 4 ; + ∞ ?
A. 2034
B. 2018
C. 2025
D. 2021
Chọn D.
ĐK: x # 1
Ta có y ' = m + 1 x 2 - 2 m + 1 x - 4 m x - 1 2
Để hàm số đồng biến trên 4 ; + ∞ thì y ' ≥ 0 ; ∀ x > 4
![]()
![]()
+ Với m + 1 = 0 ⇔ m = - 1 ⇒ 0 > - 4 (luôn đúng) nên nhận m = - 1 ( 1 )
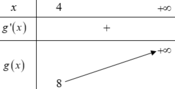
+ Với m + 1 > 0 ⇔ m > - 1
![]()
![]()
Xét hàm số g x = x 2 - 2 x có g ' x = 2 x - 2 = 0
![]()
ta có BBT trên 4 ; + ∞ là
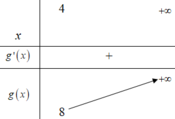
Từ BBT suy ra
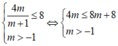
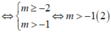
+ Với m + 1 < 0 ⇔ m < - 1
![]()
![]()
Từ BBT của g x suy ra không có m thỏa mãn.
Từ (1) và (2) suy ra m ≥ - 1 mà m ∈ - 2019 ; 2019
và m nguyên nên m ∈ - 1 ; 0 ; . . . ; 2019
⇒ có 2021 số thỏa mãn
Đúng 0
Bình luận (0)
Số các giá trị nguyên của tham
M
∈
-
2019
;
2019
để hàm số
y
m
+
1
x
2
-
2
m
x
+
6
m...
Đọc tiếp
Số các giá trị nguyên của tham M ∈ - 2019 ; 2019 để hàm số y = m + 1 x 2 - 2 m x + 6 m x - 1 đồng biến trên khoảng 4 ; + ∞ ?
A. 2034
B. 2018
C. 2025
D. 2021
ĐK: x#1
Ta có
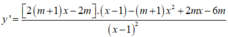
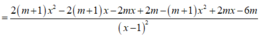
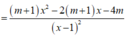
Để hàm số đồng biến trên 4 ; + ∞ thì y ' ≥ 0 ; ∀ x > 4
![]()
![]()
+ Với m+1=0 ⇔ m=-1 ⇒ 0>-4 (luôn đúng) nên nhận m=-1.(1)
+ Với m+1>0
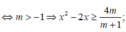
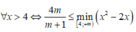
Xét hàm số g ( x ) = x 2 - 2 x có g ' ( x ) = 2 x - 2 = 0 ⇔ x = 1 ∉ 4 ; + ∞ , ta có BBT trên 4 ; + ∞ là
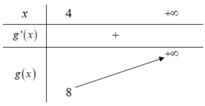
Từ BBT suy ra
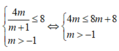
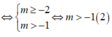
+ Với m+1<0 ⇔ m < - 1
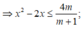
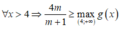
Từ BBT của g(x) suy ra không có m thỏa mãn.
Từ (1) và (2) suy ra m ≥ - 1 mà m ∈ - 2019 ; 2019 và m nguyên nên m ∈ - 1 ; 0 ; . . ; 2019 ⇒ có 2021 số thỏa mãn.
Chọn đáp án D.
Đúng 0
Bình luận (0)
Số các giá trị nguyên của tham
M
∈
[
-
2019
;
2019
]
để hàm số
y
m
+
1
x
2
-
2
m
x
+
6
m...
Đọc tiếp
Số các giá trị nguyên của tham M ∈ [ - 2019 ; 2019 ] để hàm số y = m + 1 x 2 - 2 m x + 6 m x - 1 đồng biến trên khoảng 4 ; + ∞ ?
A. 2034
B. 2018
C. 2025
D. 2021
cho hàm số y=x^2-3(m+1)x+m^2+3m-2, m là tham số . Tìm tất cả giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
Có bao nhiêu giá trị nguyên của m ∈ (-10; 10) để hàm số y = f(x) = \(\left|3x^4-4x^3-6mx^2+12mx\right|\) có đúng 3 điểm cực trị
\(g\left(x\right)=3x^4-4x^3-6mx^2+12mx\)
\(g'\left(x\right)=12x^3-12x^2-12mx+12m=0\)
\(\Leftrightarrow12x^2\left(x-1\right)-12m\left(x-1\right)=0\)
\(\Leftrightarrow12\left(x^2-m\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x^2=m\end{matrix}\right.\)
Xét \(g\left(x\right)=0\Leftrightarrow x\left(3x^3-4x^2-6mx+12m\right)=0\)
- Nếu \(m=0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ \(\Rightarrow f\left(x\right)\) có 3 cực trị (thỏa mãn)
- Nếu \(m=\dfrac{1}{6}\Rightarrow g'\left(x\right)=0\) có 3 nghiệm bội lẻ, \(g\left(x\right)=0\) có 3 nghiệm pb nhưng chỉ có 1 nghiệm \(x=1\) trùng với \(g'\left(x\right)=0\) nên hàm có 5 cực trị (ktm)
- Nếu \(m=1\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (thỏa mãn)
- Nếu \(m< 0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ \(x=1\)
Khi đó hàm có 3 cực trị khi \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (hiển nhiên từ các TH này thì \(g\left(x\right)=0\) ko thể có nghiệm \(x=1\) do đã loại trừ từ TH \(m=\dfrac{1}{6}\))
\(\Leftrightarrow3x^3-4x^2-6mx+12m=0\) có đúng 1 nghiệm
\(\Leftrightarrow3x^3-4x^2=6m\left(x-2\right)\Leftrightarrow m=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) (do \(x=2\) ko là nghiệm)
Khảo sat \(h\left(x\right)=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) ta được \(y=m\) cắt \(y=h\left(x\right)\) tại đúng 1 điểm khi: \(\left[{}\begin{matrix}m< 0\\\dfrac{1}{6}< m< \dfrac{64}{9}\\\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
- Nếu \(m>0;m\ne\left\{\dfrac{1}{6};1\right\}\) \(\Rightarrow g'\left(x\right)=0\) có 3 nghiệm pb
Mà \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm bội lẻ \(x=0\)
\(\Rightarrow\) Hàm có 3 cực trị khi và chỉ khi:
TH1: \(3x^3-4x^2-6mx+12m=0\) vô nghiệm (vô lý do hàm bậc 3 luôn có nghiệm)
Th2: \(3x^3-4x^2-6mx+12m=0\) (1) có 3 nghiệm đều trùng với nghiệm của \(g'\left(x\right)=0\) (vô lý do \(m\ne\dfrac{1}{6}\) nên nếu (1) có nghiệm thì nó luôn có nghiệm khác 1)
Kết luận: \(\left[{}\begin{matrix}m=1\\m\le0\end{matrix}\right.\)
Đúng 0
Bình luận (3)
Cho hàm số
y
f
(
x
)
x
-
m
2
x
+
4
với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1 A. m 2 B. m 0 C.
m
6
D. m 3
Đọc tiếp
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3