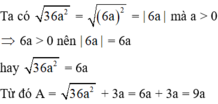4a2b2+36a2+6ab

Những câu hỏi liên quan
Rút gọn các biểu thức sau:
9
+
12
a
+
4
a
2
b
2
v
ớ
i
a
≥
-
1
,
5
v
à
b
0
Đọc tiếp
Rút gọn các biểu thức sau: 9 + 12 a + 4 a 2 b 2 v ớ i a ≥ - 1 , 5 v à b < 0
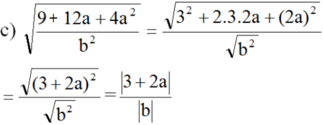
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
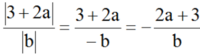
Đúng 0
Bình luận (0)
Rút gọn biểu thức A = 36 a 2 + 3 a với a > 0
A. −9a
B. −3a
C. 3a
D. 9a
Phân tích
a
2
+
9
2
-
36
a
2
thành nhân tử ta được A.
(
a
–
3
)
2
(...
Đọc tiếp
Phân tích a 2 + 9 2 - 36 a 2 thành nhân tử ta được
A. ( a – 3 ) 2 ( a + 3 ) 2
B. ( a + 3 ) 4
C. ( a 2 + 36 a + 9 ) ( a 2 – 36 a + 9 )
D. a 2 + 9 2
Ta có
( a 2 + 9 ) 2 – 36 a 2 = ( a 2 + 9 ) 2 – ( 6 a ) 2 = ( a 2 + 9 + 6 a ) ( a 2 + 9 – 6 a ) = ( a + 3 ) 2 ( a – 3 ) 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
a) 25x2 - 20xy + 4y
b) 1/36a2 - 1/4b2
c) 0.125 (a+2)3 - 1
d) x6 - 1
\(a,Sửa:25x^2-20xy+4y^2=\left(5x-2y\right)^2\\ b,=\dfrac{1}{4}\left(\dfrac{1}{9}a^2-b^2\right)=\dfrac{1}{4}\left(\dfrac{1}{3}a-b\right)\left(\dfrac{1}{3}a+b\right)\\ c,=\dfrac{1}{8}\left(a+2\right)^3-1=\left[\dfrac{1}{2}\left(a+2\right)\right]^3-1=\left[\dfrac{1}{2}a+1\right]^3-1\\ =\left(\dfrac{1}{2}a+1-1\right)\left(\dfrac{1}{4}a^2+a+1+\dfrac{1}{2}a+1+1\right)\\ =\dfrac{1}{2}a\left(\dfrac{1}{4}a^2+\dfrac{3}{2}a+3\right)\\ d,=\left(x^3-1\right)\left(x^3+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)\)
Đúng 5
Bình luận (0)
Tìm hệ số trong đơn thức
-
36
a
2
.
b
2
.
x
2
.
y
3
với a, b là hằng số A. -36 B.
-
36
a
2
b
2
C.
36
a
2
b
2
D.
-...
Đọc tiếp
Tìm hệ số trong đơn thức - 36 a 2 . b 2 . x 2 . y 3 với a, b là hằng số
A. -36
B. - 36 a 2 b 2
C. 36 a 2 b 2
D. - 36 a 2
Đơn thức - 36 a 2 . b 2 . x 2 . y 3 với a, b là hằng số có hệ số là - 36 a 2 . b 2
Chọn đáp án B
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau:
a
)
a
b
2
3
a
2
b
4
v
ớ
i
a
0
;
b
≠
0
b
)
27...
Đọc tiếp
Rút gọn các biểu thức sau:
a ) a b 2 3 a 2 b 4 v ớ i a < 0 ; b ≠ 0 b ) 27 a - 3 2 48 v ớ i a > 3 c ) 9 + 12 a + 4 a 2 b 2 v ớ i a ≥ - 1 , 5 v à b < 0 d ) a - b a b a - b 2 v ớ i a < b < 0
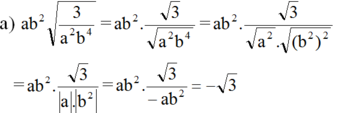
(vì a < 0 nên |a| = -a, b2 > 0 với mọi b ≠ 0 nên |b2| = b2 )
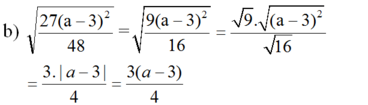
(vì a > 3 nên |a - 3| = a - 3)
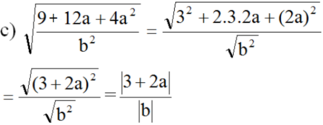
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
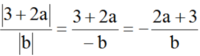
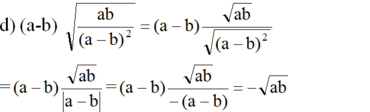
(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử: a) 50x5-8x3 b) x4-5x2-4y2+10yc) 36a2-b2+12a+1d) x3+y3-xy2-x2ye) 4x2+4x-3f) 9x4+16x2-4g) -6x2+5xy+4y2h)(x2+4x)2+8(x2+4x)+15i) 9x4+5x2+1
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) 50x5-8x3
b) x4-5x2-4y2+10y
c) 36a2-b2+12a+1
d) x3+y3-xy2-x2y
e) 4x2+4x-3
f) 9x4+16x2-4
g) -6x2+5xy+4y2
h)(x2+4x)2+8(x2+4x)+15
i) 9x4+5x2+1
a: \(50x^5-8x^3\)
\(=2x^3\left(25x^2-4\right)\)
\(=2x^3\left(5x-2\right)\left(5x+2\right)\)
b: \(x^4-5x^2-4y^2+10y\)
\(=\left(x^2-2y\right)\left(x^2+2y\right)-5\left(x^2-2y\right)\)
\(=\left(x^2-2y\right)\left(x^2+2y-5\right)\)
c: \(36a^2+12a+1-b^2\)
\(=\left(6a+1\right)^2-b^2\)
\(=\left(6a+1-b\right)\left(6a+1+b\right)\)
d: \(x^3+y^3-xy^2-x^2y\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-2xy+y^2\right)\)
\(=\left(x+y\right)\cdot\left(x-y\right)^2\)
Đúng 0
Bình luận (0)
e: Ta có: \(4x^2+4x-3\)
\(=4x^2+6x-2x-3\)
\(=2x\left(2x+3\right)-\left(2x+3\right)\)
\(=\left(2x+3\right)\left(2x-1\right)\)
f: Ta có: \(9x^4+16x^2-4\)
\(=9x^4+18x^2-2x^2-4\)
\(=9x^2\left(x^2+2\right)-2\left(x^2+2\right)\)
\(=\left(x^2+2\right)\left(9x^2-2\right)\)
g: Ta có: \(-6x^2+5xy+4y^2\)
\(=-6x^2+8xy-3xy+4y^2\)
\(=-2x\left(3x-4y\right)-y\left(3x-4y\right)\)
\(=\left(3x-4y\right)\left(-2x-y\right)\)
h: Ta có: \(\left(x^2+4x\right)^2+8\left(x^2+4x\right)+15\)
\(=\left(x^2+4x\right)^2+3\left(x^2+4x\right)+5\left(x^2+4x\right)+15\)
\(=\left(x^2+4x+3\right)\cdot\left(x^2+4x+5\right)\)
\(=\left(x+1\right)\left(x+3\right)\left(x^2+4x+5\right)\)
Đúng 0
Bình luận (0)
Tìm hai số tự nhiên a , b :
a) 6ab - a + 4b - 2 = 0
b) 6ab - 4a - 3b + 1 = 0
6ab = ab x41
6ab=abx41
600+ab=abx41
abx(41-1)=600
abx40=600
ab=15
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho 8a^2+b^2=6ab
Hãy tính giá trị của phân thức M=a^2+b^2+3ab/a^2-b^2+6ab