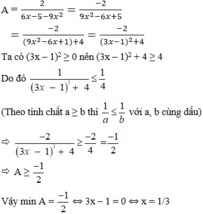tìm giá trị nhỏ nhất 9x2 -12x+10
MH
Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của biểu thức:
a) x 2 – 8x + 17
b) 4x2 – 12x + 13
c) 9x2 – 2x + 3
\(a,=x^2-8x+16+1=\left(x-4\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow x=4\)
\(b,=\left(4x^2-12x+9\right)+4=\left(2x-3\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(c,=\left(9x^2-2\cdot3\cdot\dfrac{1}{3}x+\dfrac{1}{9}\right)+\dfrac{26}{9}=\left(3x-\dfrac{1}{3}\right)^2+\dfrac{26}{9}\ge\dfrac{26}{9}\)
Dấu \("="\Leftrightarrow3x=\dfrac{1}{3}\Leftrightarrow x=\dfrac{1}{9}\)
Đúng 2
Bình luận (0)
tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức sau
a) 25x2-20x+7
b)9x2-6x+2
c)-x2+2x-2
d)x2+12x+39
e)-x2-12x
f)4x-x2+1
a) Ta có: \(25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{5}\)
b) Ta có: \(9x^2-6x+2\)
\(=9x^2-6x+1+1\)
\(=\left(3x-1\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{3}\)
c) Ta có: \(-x^2+2x-2\)
\(=-\left(x^2-2x+2\right)\)
\(=-\left(x^2-2x+1+1\right)\)
\(=-\left(x-1\right)^2-1\le-1\forall x\)
Dấu '=' xảy ra khi x-1=0
hay x=1
d) Ta có: \(x^2+12x+39\)
\(=x^2+12x+36+3\)
\(=\left(x+6\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi x=-6
e) Ta có: \(-x^2-12x\)
\(=-\left(x^2+12x+36-36\right)\)
\(=-\left(x+6\right)^2+36\le36\forall x\)
Dấu '=' xảy ra khi x=-6
f) Ta có: \(4x-x^2+1\)
\(=-\left(x^2-4x-1\right)\)
\(=-\left(x^2-4x+4-5\right)\)
\(=-\left(x-2\right)^2+5\le5\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 1
Bình luận (0)
tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức sau
a) 25x2-20x+7
b)9x2-6x+2
c)-x2+2x-2
d)x2+12x+39
e)-x2-12x
f)4x-x2+1
a) Ta có: \(25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{5}\)
b) Ta có: \(9x^2-6x+2\)
\(=9x^2-6x+1+1\)
\(=\left(3x-1\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{3}\)
c) Ta có: \(-x^2+2x-2\)
\(=-\left(x^2-2x+2\right)\)
\(=-\left(x^2-2x+1+1\right)\)
\(=-\left(x-1\right)^2-1\le-1\forall x\)
Dấu '=' xảy ra khi x=1
Đúng 1
Bình luận (0)
( Mình trình bày mẫu câu a các câu khác mình làm tắt lại nhưng tương tự trình bày câu a nha )
a, Ta có : \(25x^2-20x+7=\left(5x\right)^2-2.5x.2+2^2+3\)
\(=\left(5x-2\right)^2+3\)
Thấy : \(\left(5x-2\right)^2\ge0\forall x\in R\)
\(\Rightarrow\left(5x-2\right)^2+3\ge3\forall x\in R\)
Vậy \(Min=3\Leftrightarrow5x-2=0\Leftrightarrow x=\dfrac{2}{5}\)
b, \(=9x^2-2.3x+1+1=\left(3x-1\right)^2+1\ge1\)
Vậy Min = 1 <=> x = 1/3
c, \(=-x^2+2x-1-1=-\left(x^2-2x+1\right)-1=-\left(x-1\right)^2-1\le-1\)
Vậy Max = -1 <=> x = 1
d, \(=x^2+2.x.6+36+3=\left(x+6\right)^2+3\ge3\)
Vậy Min = 3 <=> x = - 6
e, \(=-x^2-2.x.6-36+36=-\left(x+6\right)^2+36\le36\)
Vậy Max = 36 <=> x = -6 .
f, \(=-x^2+4x-4+5=-\left(x^2-4x+4\right)+5=-\left(x-2\right)^2+5\le5\)
Vậy Max = 5 <=> x = 2
Đúng 1
Bình luận (0)
Giúp vs ạ
9x2+10y2+24z2-6xy-20xyz-12xz-12x-8y+16z+22 tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất của phân thức A = 2 6 x - 5 - 9 x 2
Hàm số y 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình
2
x
3
-
9
x
2
+
12
x
+
m
0
có sáu nghiệm phân biệt. A.m - 5 B. -5 m- 4 C. 4 m 5 D.m -4
Đọc tiếp
Hàm số y= 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 có sáu nghiệm phân biệt.
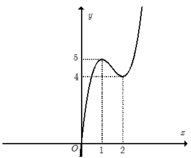
A.m< - 5
B. -5< m<- 4
C. 4< m< 5
D.m> -4
+Trước tiên từ đồ thị hàm số y= 2x3- 9x2+12x , ta suy ra đồ thị hàm số y= 2 x 3 - 9 x 2 + 12 x như hình dưới đây:
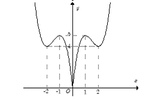
+ Phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 và đường thẳng y= -m
+ Dựa vào đồ thị hàm số y = 2 x 3 - 9 x 2 + 12 x , yêu cầu bài toán trở thành:
4< -m< 5 hay -5<m< -4.
Chọn B.
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức sau : A=\(4x^2-12x+10\)
ta có 4X2-12X+10= 4X2-2*2*3X+32+1=(2X-3)2+1
(2x-3)2>=0 => ( 2X-3)2+1>=1
Biểu thức đạt giá trị nhỏ nhất là 1
khi đó 2X-3=0 => X=3/2
Đúng 0
Bình luận (0)
Ta có: 4x^2 - 12x + 10 = 4x^2 - 6x - 6x +9 + 1= [2x(2x-3) - 3(2x-3)] + 1 = (2x-3)^2 + 1
để (2x-3)^2 + 1 bé nhất thì (2x-3)^2 bé nhất => (2x-3)^2= 0 => (2x-3)^2 + 1 = 1
Vậy giá trị bé nhất của A=.. là 1
Đúng 0
Bình luận (0)
4x^2-12x+10
=4x^2-12x+9+1
=(2x-3)^2+1
Ma: (2x-3)^2 >=1
=> (2x-3)^2+1>=1
Vay GTNN la 1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho f(x)=4x^2-12x+10
tìm x để f(x) thuộc giá trị nhỏ nhất
\(f\left(x\right)=4x^2-12x+10\)
=> \(f\left(x\right)=4\left(x^2-3x\right)+10\)
=> \(f\left(x\right)=4\left(x^2-2.x.\frac{3}{2}+\frac{9}{4}\right)-9+10\)
=> \(f\left(x\right)=4.\left(x-\frac{3}{2}\right)^2+1\)
Có: \(\left(x-\frac{3}{2}\right)^2\ge0\)với mọi x
=> \(4.\left(x-\frac{3}{2}\right)^2\ge0\)với mọi x
=> \(4.\left(x-\frac{3}{2}\right)^2+1\ge1\)với mọi x
=> \(f\left(x\right)\ge1\)với mọi x
Dấu "-" xảy ra <=> \(\left(x-\frac{3}{2}\right)^2=0\)
<=> \(x-\frac{3}{2}=0\)
<=> \(x=\frac{3}{2}\)
KL: GTNN của f(x) = 1 <=> \(x=\frac{3}{2}\)
Đúng 0
Bình luận (0)
4x2-12x+Vậy = [(2x)2-2.2x.3+32]+1
= (2x+3)2+1 >= 1
Vậy GTNN của f(x) bằng 1 khi và chỉ kho 2x+3=0 => x=-3/2
k đúng hộ mình ^^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
CMR giá trị của các biểu thức sau không âm với mọi giá trị của biến x: A=x2 –3x+10 B = x2 – 5x + 2021 C = 4x2 + 4x + 5 D = 9x2 – 12x + 6
a: ta có: \(A=x^2-3x+10\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{31}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}>0\forall x\)
b: Ta có: \(B=x^2-5x+2021\)
\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{8015}{4}\)
\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{8015}{4}>0\forall x\)
Đúng 2
Bình luận (0)