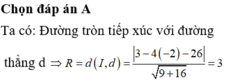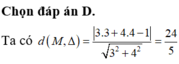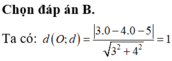Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x - 4y - 1 = 0 và điểm I(1;- 2) . Gọi (C) là đường tròn tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Viết phương trình đường tròn (C).
HJ
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, tính bán kính đường tròn tâm I(1;-2) và tiếp xúc với đường thẳng d: 3x-4y-26=0
A. R = 3
B. R = 5
C. R = 9.
D. R = 3 5
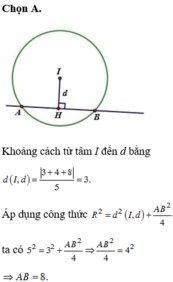
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có tâm I(1;-1) và bán kính R=5. Biết rằng đường thẳng ( d ) : 3 x - 4 y + 8 = 0 cắt đường tròn (C) tại hai điểm phân biệt A, B. Tính độ dài đoạn thẳng AB
A. 8
B. 4
C. 3
D. 6
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d có phương trình
3
x
+
4
y
+
6
0
là ảnh của đường thẳng d có phương trình
3
x
+
4
y
+
1
0
qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
v
→
có độ dài bé nhất. A....
Đọc tiếp
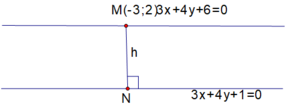
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d' có phương trình 3 x + 4 y + 6 = 0 là ảnh của đường thẳng d có phương trình 3 x + 4 y + 1 = 0 qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ v → có độ dài bé nhất.
A. v → = 3 5 ; − 4 5
B. v → = − 3 5 ; − 4 5
C. v → = ( 3 ; 4 )
Đáp án B
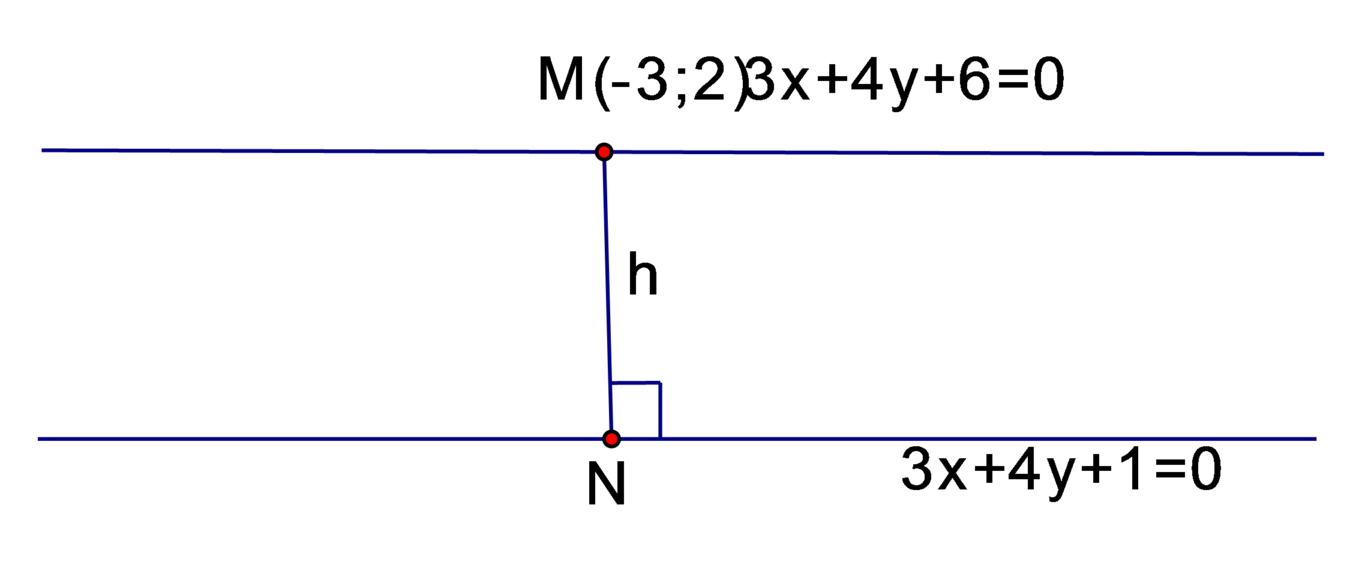
Độ dài véc tơ v → bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó: v → = M N →
Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:
M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3
⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5
⇒ M N → = − 3 5 ; − 4 5
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d có phương trình 3x+4y+60 là ảnh của đường thẳng d có phương trình 3x+4y+10 qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
v
→
có độ dài bé nhất. A.
v
→
3
5
;
-...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d có phương trình 3x+4y+6=0 là ảnh của đường thẳng d có phương trình 3x+4y+1=0 qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ v → có độ dài bé nhất.
A. v → = 3 5 ; - 4 5
B. v → = - 3 5 ; - 4 5
C. v → = 3 ; 4
D. v → = - 3 ; 4
Trong mặt phẳng tọa độ Oxy, khoảng cách từ điểm M(3;-4) đến đường thẳng
△
:
3
x
-
4
y
-
1
0
là A.
12
5
B.
8
5
C.
-
24
5
D.
24
5
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, khoảng cách từ điểm M(3;-4) đến đường thẳng △ : 3 x - 4 y - 1 = 0 là
A. 12 5
B. 8 5
C. - 24 5
D. 24 5
Trong mặt phẳng tọa độ Oxy, khoảng cách từ điểm O(0;0) đến đường thẳng d: 3x-4y-5=0 là:
A. - 1 5
B. 1 5
C. 0.
D. 1.
Trong mặt phẳng tọa độ Oxy, cho điểm C(2; -5) và đường thẳng D:3x-4y+40. Trên đường thẳng D hai điểm A và B đối xứng nhau qua điểm
I
2
;
5
2
sao cho diện tích tam giác ABC bằng 15. Tìm tọa độ điểm A biết điểm B có hoành độ dương. A. A(8; 7) B. A(4; 4) C. A(0; 1) D. A(-4; -2
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm C(2; -5) và đường thẳng D:3x-4y+4=0. Trên đường thẳng D hai điểm A và B đối xứng nhau qua điểm I 2 ; 5 2 sao cho diện tích tam giác ABC bằng 15. Tìm tọa độ điểm A biết điểm B có hoành độ dương.
A. A(8; 7)
B. A(4; 4)
C. A(0; 1)
D. A(-4; -2
Trong mặt phẳng hệ tọa độ oxy, cho đường tròn (C):(x-2)2+(y-3)2=100 và đường thẳng denta:3x-4y+1=0.Gọi A,B là hai giao điểm của denta và(C).Tính độ dài đoạn thẳng AB
Đường tròn (C) tâm \(O\left(2;3\right)\) bán kính \(R=10\)
Gọi I là trung điểm AB \(\Rightarrow IO\perp AB\)
\(\Rightarrow IO=d\left(O;AB\right)=\dfrac{\left|3.2-4.3+1\right|}{\sqrt{3^2+4^2}}=1\)
Áp dụng định lý Pitago:
\(IA=\sqrt{OA^2-OA^2}=\sqrt{100-1}=3\sqrt{11}\)
\(\Rightarrow AB=2IA=6\sqrt{11}\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy , cho đường thẳng d: 3x-4y+1=0 . Thực hiện liên tiếp phép vị tự tâm O tỉ số k=-3 và phép tịnh tiến theo vecto v=(1,2) thì đường thẳng d biến đường thẳng d' có phương trình là ?
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C) có phương trình
x
-
2
2
+
y
+
2
2
4
và đường thẳng
d
:
3
x
+
4
y
+
7
0
. Gọi A B, là các...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C) có phương trình x - 2 2 + y + 2 2 = 4 và đường thẳng d : 3 x + 4 y + 7 = 0 . Gọi A B, là các giao điểm của đường thẳng d với đường tròn (C) . Tính độ dài dây cung AB.
A. AB = 3 .
B. AB = 2 5 .
C. AB = 2 3 .
D. AB = 4 .