nêu cách chứng minh 2 đường thẳng song song
LL
Những câu hỏi liên quan
Nêu các cách chứng minh 2 đường thẳng song song
Nêu phương pháp chứng minh Đường thẳng song song với đường thẳng
hứng minh đường thẳng song song với đường thẳng:
Để chứng minh hai đường thẳng song song, ta sử dụng các định lí.
- Ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng qui hoặc đôi một song song với nhau.
- Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
- Cho đường thẳng d song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa d và cắt (α) theo giao tuyến d’ thì d’ song song với d.
- Hai mặt phẳng phân biệt cùng song song với với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Một mặt phẳng cắt hai mặt phẳng song song cho hai giao tuyến song song.
- Sử dụng các phương pháp của hình học phẳng. Tính chất đường trung bình, định lí Ta-lét đảo, cạnh đối hình bình hành…
- Sử dụng tính chất về cạnh bên, cạnh đáy của hình lăng trụ.
Đúng 0
Bình luận (0)
1, nêu tất cả các cách xác định mặt phẳng2, nêu tất cả các quy tắc vẽ hình biểu diễn ( kể cả phép chiếu song song)3, nêu các cách xác định giao tuyến, giao điểm của 2 đường thẳng + đường thẳng và mặt phẳng4, nêu các phương pháp chứng mình 2 đường thẳng song song5, nêu các phương pháp chứng mình đưởng thẳng // mp6, nêu các phương pháp chứng mình mp//mp7, cách xác định góc giữa 2 đưởng thẳng bất kì trong không gian
Đọc tiếp
1, nêu tất cả các cách xác định mặt phẳng
2, nêu tất cả các quy tắc vẽ hình biểu diễn ( kể cả phép chiếu song song)
3, nêu các cách xác định giao tuyến, giao điểm của 2 đường thẳng + đường thẳng và mặt phẳng
4, nêu các phương pháp chứng mình 2 đường thẳng song song
5, nêu các phương pháp chứng mình đưởng thẳng // mp
6, nêu các phương pháp chứng mình mp//mp
7, cách xác định góc giữa 2 đưởng thẳng bất kì trong không gian
Nêu phương pháp chứng minh :
- Đường thẳng song song với đường thẳng
- Đường thẳng song song với mặt phẳng
- Mặt phẳng song song với mặt phẳng
Muốn chứng minh đường thẳng a // (P), ta chứng minh đường thẳng a song song với đường thẳng b mà đường thẳng b song song với mặt phẳng (P) (a và (P) không có điểm chung)
Đúng 0
Bình luận (0)
Nêu phương pháp chứng minh Đường thẳng song song với mặt phẳng
Chứng minh đường thẳng song song với mặt phẳng
- Chứng minh d song song với đường thẳng d’ nằm trong (α) và d không thuộc(α).
- Có hai mặt phẳng song song, bất kì đường nào nằm trong hai mặt phẳng này cũng song song với mặt phẳng kia.
Đúng 0
Bình luận (0)
Làm sao để chứng minh hai đường thẳng song song? Cách làm chứng minh hai đường thẳng song song ? Mong các bạn có thể giải đáp câu trả lời của mình .
- Hai đường thẳng cùng thẳng góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
- Một đường thẳng cắt hai đường thẳng mà trong các góc tạo thành có các cặp góc: Đồng vị hay so le trong bằng nhau thì hai đường thẳng bị cắt là hai đường thẳng song song.
- Một đường thẳng cắt hai đường thẳng và định ra trên hai đường thẳng đó những đoạn thẳng tương ứng tỷ lệ bằng nhau, thì hai đường thẳng đó song song nhau.
- Hai đường thẳng cùng song song với một đường thẳng thứ ba, thì hai đường thẳng đó song song nhau.
Đúng 0
Bình luận (0)
Hai đường thẳng song song là hai đường thẳng đối diện nhau
Ko có điểm chung nào
Đúng 0
Bình luận (0)
Cảm ơn các bạn nhé ^^, nhưng ý mình là cách chứng minh hai đường thẳng song song ấy, ý mình là cách làm bài chứng mình 2 đường song song. Mấy bạn có thể giúp mình được không ạ !
Đúng 0
Bình luận (0)
Viết giả thiết, kết luận, vẽ hình và chứng minh định lí sau:
Cho hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau (làm 2 cách)
Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau.
Chứng minh rằng:
a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.
b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.
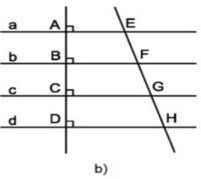
a) Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD
⇒ B là trung điểm của AC; C là trung điểm của BD
- Hình thang AEGC (AE // GC) có B là trung điểm của AC và BF song song hai cạnh đáy
⇒ F là trung điểm EG (định lí đường trung bình của hình thang)
⇒ EF = FG
- Chứng minh tương tự ⇒ G là trung điểm FH
⇒ FG = GH
Vậy EF = FG = GH
Đúng 0
Bình luận (0)
Cho hình vẽ bên.a) Chứng minh AD song song với BC.b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm E sao cho 70°. Chứng minh E, A, D thẳng hàng theo hai cách sau:Cách 1: Chứng minh 180°.Cách 2: Sử dụng tiên đề Ơ-clit.
Đọc tiếp
Cho hình vẽ bên.
a) Chứng minh AD song song với BC.
b) Trên nửa mặt phẳng có bờ là đường thẳng AB không chứa điểm D, lấy điểm E sao cho = 70°. Chứng minh E, A, D thẳng hàng theo hai cách sau:
Cách 1: Chứng minh = 180°.
Cách 2: Sử dụng tiên đề Ơ-clit.
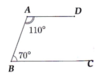
a) Ta có D A B ^ + A B C ^ = 180°.
Mà hai góc ở vị trí trong cùng phía.
Từ đó AD // BC (tính chất hai đường thẳng song song).
b) Cách 1:
E A B ^ + B A D ^ = 70° + 110° = 180°
Cách 2: E A B ^ = A B C ^ = 70°
Mà hai góc ở vị trí so le trong nên AE// BC ( tính chất hai đường thẳng song song)
Lại có AD//BC ( chứng minh ý a)) nên Ad = AE.
Vậy E, A, D thẳng hàng
Đúng 0
Bình luận (0)



