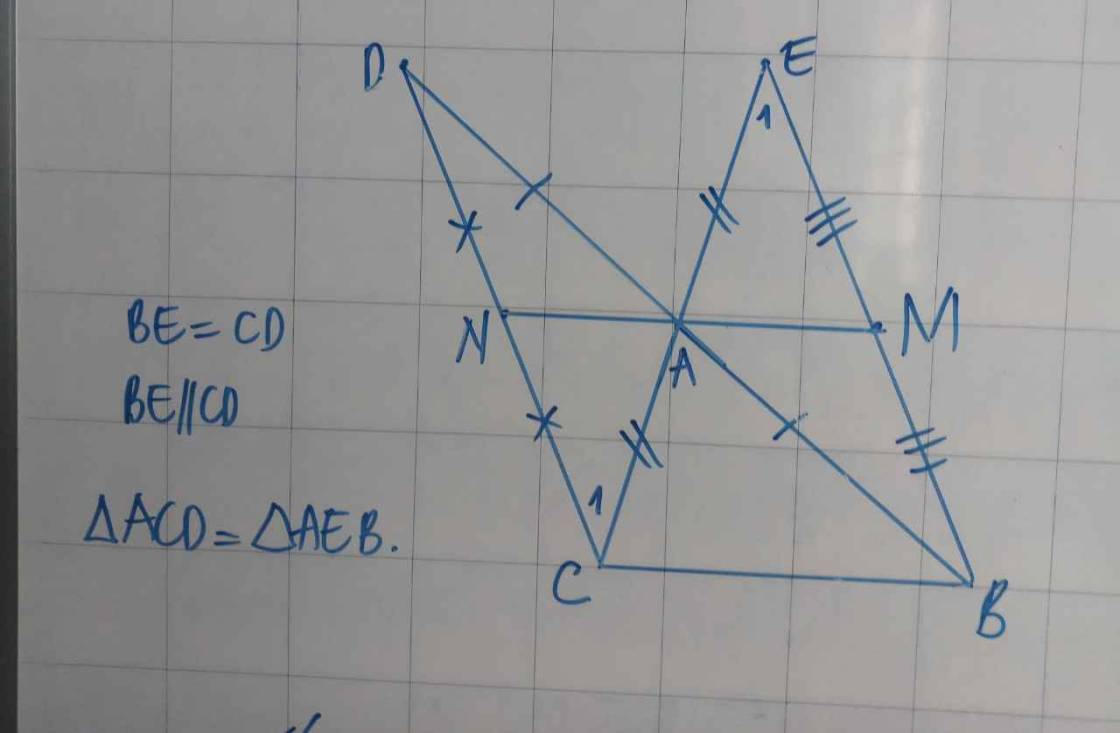
 Chứng minh AM = AN
Chứng minh AM = AN
MD
Những câu hỏi liên quan
Cho tam giác nhọn ABC : Vẽ điểm E thuộc AC . Vẽ điểm K thuộc AB . M thuộc tia CK : CK=KM .N thuộc tia BE:BE=EN
a, chứng minh AM=BC
b, chứng minh AN=BC
c, chứng minh AM=AN
d,chứng minh AM//BC
e,chứng minh AN//BC
g,chứng minh M;A;N thẳng hàng
h,chứng minh A là trung điểm của MN
a)Tam giác MAK =tgKCB(c.g.c) (1) ->AM=BC (2 cạnh tương ứng ) b) tg ANE=tg EBC (c.g.c) (2) ->AN=BC (2 cạnh tương ứng) c) vì AN =BC , AM=BC ->AN=AM
d) từ (1) suy ra góc AMK =góc KCB (2 góc t ứng )
Mà chúng ở vị trí so le trong suy ra AM//BC
e) từ (2) -> góc ANE =góc EBC (2 góc t ứng ) mà chúng ở vị trí so le trong -> AN//BC
g) vì AN//BC , AM//BC -> A,N,N thẳng hàng (3)
Mà MA= BC , AN =BC
-> MA=AN (4)
Từ (3) , (4) -> A là trung điểm của MN
Đúng 0
Bình luận (0)
Bài 3: Cho ABC (AB = AC). Gọi M là trung điểm của BC.
a) Chứng minh: AM là phân giác của BAC .
b) Trên nửa mặt phẳng không chứa B có bờ AM, vẽ tia Ax vuông góc với AM,
lấy N thuộc tia Ax sao cho AN = MC. Chứng minh: AN // BC.
c) Chứng minh: BAM = ACN.
d) Gọi O là trung điểm của AC. Chứng minh O là trung điểm MN.
a: ta có: ΔACB can tại A
mà AM là đường trung tuyến
nên AM là đường p/g
Đúng 0
Bình luận (0)
cho tam giác ABC có ABAC M là trung điểm của BC Chứng minh AM là phân giác của góc BAC chứng minh AM vuông góc với BC chứng minh M là trung điểm của AN
Đọc tiếp
cho tam giác ABC có AB=AC M là trung điểm của BC Chứng minh AM là phân giác của góc BAC chứng minh AM vuông góc với BC chứng minh M là trung điểm của AN
Cho hình thoi ABCD. Từ A hạ 2 đường cao AM và AN xuống các cạnh BC;DC. Chứng minh AM=AN
Bài 9: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm Nsao cho BM CN.a) Chứng minh rằng tam giác AMN là tam giác cânb) Kẻ BH ⊥ AM (H ∊ AM), kẻ CK ⊥ AN (K ∊ AN). Chứng minh rằng BH CKc) Chứng minh rằng AH AKd) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?Bài 10: Cho tam giác ABC vuông tại A có AB 6cm; AC 8cm.a) Tính độ dài đoạn thẳng BCb) Vẽ tia phân giác BD của góc B. Từ D kẻ DE BC ⊥ tại E.Chứng minh ABD EBDc) Ch...
Đọc tiếp
Bài 9: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N
sao cho BM = CN.
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH ⊥ AM (H ∊ AM), kẻ CK ⊥ AN (K ∊ AN). Chứng minh rằng BH = CK
c) Chứng minh rằng AH = AK
d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
Bài 10: Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm.
a) Tính độ dài đoạn thẳng BC
b) Vẽ tia phân giác BD của góc B. Từ D kẻ DE BC ⊥ tại E.
Chứng minh = ABD EBD
c) Chứng minh: Tam giác ABE là tam giác cân
Bài 11: Cho ABC vuông tại A. BE là tia phân giác của góc ABC (E AC . ) Kẻ EI BC ⊥ (I BC . )
a) Chứng minh = ABE IBE
b) Tia IE và tia BA cắt nhau tại M. Chứng minh EMC cân
c) Chứng minh AI // MC
Bài 12: Cho ABC vuông tại B (AC AB . ) D là điểm thuộc AC sao cho AB = AD. Kẻ AH BD ⊥ tại
H, AH cắt BC tại E.
| a) Chứng minh b) Chứng minh cân | c) Giả sử Tính cạnh BC? |
= ABH ADH
EBD BED 120 , = o AB 2cm. = Bài 13: Cho ABC vuông tại C có A 60 = o và đường phân giác của BAC cắt BC tại E. Kẻ EK AB ⊥
tại K (K AB . ) Kẻ BD AE ⊥ tại D (D AE . ) Chứng minh:
| a) | c) KA = KB |
| b) AE là đường trung trục của đoạn thẳng CK | d) EB > EC |
= ACE AKE Bài 14: Cho tam giác ABC cân tại A. Kẻ BE, CF lần lượt vuông góc với AC và AB (E AC F AB , )
a) Chứng minh = ABE ACF
b) Gọi I là giao điểm của BE và CF. Chứng minh BIC cân
c) So sánh FI và IC
d) Gọi M là trung điểm của BC. Chứng minh A, I, M thẳng hàng.
Bài 15: Cho tam giác ABC cân tại A có BAC = 1200 . Lấy D E , bên cạnh BC , sao BAD CAE = = 300 .
| a) là tam giác gì? Vì sao? | b) là tam giác gì? Vì sao? |
DAB DAE
Bài 9:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
hay ΔAMN cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK
c: Ta có: ΔAHB=ΔAKC
nên AH=AK
Cho tam giác ABC có BC = a, các đường trung tuyến BD, CE. Lấy các điểm M, N trên cạnh BC sao cho BM = MN = NC. Gọi I là giao điểm của AM và BD, K là giao điểm
của AN và CE.
a) Chứng minh: EM // AN và 2EM = AN.
b) Chứng minh: DN // AM và 2DN = AM.
c) Chứng minh tứ giác BEDC là hình thang.
d) Chứng minh I là trung điểm của BD, K là trung điểm của EC.
e) Tính độ dài IK theo a.
Cho tam giác ABC có ABAC. Trên tia đối của tia BC lấy điểm M và trên tia đối của CB lấy điểm N sao cho BMCN.a) Chứng minh AMANb) Kẻ BE vuông góc với AM, CF vuông góc với AN (E thuộc AM, F thuốc AN). Chứng minh tam giác BME tam giác CNFc) EB và FC kéo dài cắt nhau tại O. Chứng minh AO là phân giác của góc MAN.d) Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau tại H. Chứng minh 3 điểm A,O,H thẳng hàng
Đọc tiếp
Cho tam giác ABC có AB=AC. Trên tia đối của tia BC lấy điểm M và trên tia đối của CB lấy điểm N sao cho BM=CN.
a) Chứng minh AM=AN
b) Kẻ BE vuông góc với AM, CF vuông góc với AN (E thuộc AM, F thuốc AN). Chứng minh tam giác BME= tam giác CNF
c) EB và FC kéo dài cắt nhau tại O. Chứng minh AO là phân giác của góc MAN.
d) Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau tại H. Chứng minh 3 điểm A,O,H thẳng hàng
a)ta có AB=AC
=)TAM giác ABC cân tại A
=)Góc B2=góc C1
Lại có B1+B2=180độ(kề bù)
C1+C2=180độ(kề bù)
mà B2=C1(cmt)
=)B1=C2
Xét tam giác ABM và tam giác ACN có
BM=CN(GT)
B1=C2(CMT)
AB=AC(GT)
=)TAM giác ABM = tam giác ACN (c-g-c)
=)AM=AN(2 cạnh tương ứng )
bạn tự viết kí hiệu nhá mik ko bít cách viết
b)ta có tam giác ABM=tam giác ACN (cmt)
=)góc M=góc N (2 góc tương ứng)
xét tam giác vuông BME và tam giác vuông CNF có
BM=CN(gt)
góc M=GÓC N(cmt)
=)tam giác vuông BME=tam giác vuông CNF (cạnh huyền-góc nhọn)
c)gọi H là giao điểm của BC và AO
xét tam giác BHA và tam giac CHA
AH chung
AB=AC(GT)
B2=C1(CMT)
=)TAM GIÁC BHA=tam giác CHA(c-g-c)
=)HC=HB(2 cạnh tương ứng)
Mà tam giác ABC cân tại A (cmt)
=)AH hay AO là tia phân giác của GÓC BAC (trong tam giác cân đường trung tuyến là đường phân giác)
Lại có tam giác ABM=tam giác ACM (cmt)
=)góc A1 = GÓC A4
có A2=A3 ( AO là phân giác của góc BAC)
=)A1+A2=A3+A4
=) AO là tia phân giác góc MAN
Xem thêm câu trả lời
ChoAMN cân tại A.VẽđườngAH vuông góc với MN (HMN)
a)Chứng minh rằng AH là tia phân giác của góc MAN.
b)KẻHD vuông góc với AM (DAM),kẻHE vuông góc với AN (EAN).Chứng minhADEcân.
a) Xét t/giác AMH và t/giác ANH
có: AM = AN (gt)
\(\widehat{M}=\widehat{N}\)(gt)
\(\widehat{AHM}=\widehat{AHN}=90^0\)(gt)
=> t/giác AMH = t/giác ANH (ch - gn)
=> \(\widehat{MAH}=\widehat{NAH}\) (2 góc t/ứng)
=> AH là tia p/giác của góc MAN
b) Xét t/giác ADH và t/giác AEH
có: AH : chung
\(\widehat{DAH}=\widehat{EAH}\) (cmt)
\(\widehat{ADH}=\widehat{AEH}=90^0\)(gt)
=> t/giác ADH = t/giác AEH (ch.gn)
=> AD = AE( 2 cạnh t/ứng)
=> t/giác ADE cân tại A
a) Xét \(\Delta AHM\)và \(\Delta AHN\)có:
\(AM=AN\)( \(\Delta AMN\)cân tại A )
AH là cạnh chung
\(\widehat{AHM}=\widehat{AHN}\left(=90^0\right)\)
\(\Rightarrow\Delta AHM=\Delta AHN\left(ch.gn\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)( 2 góc tương ứng )
=> AH là tia phân giác \(\widehat{MAN}\)( đpcm )
a) Có tam gim giác AMN cân tại A (gt); AH là đường cao của \(\Delta\)ABC (AH _|_ MN)
=> AH đồng thời là đường phân giác
=> AH là phân giác \(\widehat{MAN}\) => \(\widehat{MAH}=\widehat{HAN}\)
b) Xét tam giác AHD và AHE có:
\(\widehat{HDA}=\widehat{HEA}=90^o\)
AH chung
\(\widehat{MAH}=\widehat{HAN}\left(cmt\right)\)
=> \(\Delta AHD=\Delta AHE\left(ch-gn\right)\)
=> AD=AE (2 cạnh tương ứng)
=> Tam giác ADE cân tại A (đpcm)
Xem thêm câu trả lời
Bài 5:(2,5đ) Cho △ABC cân tại.A. Tia phân giác góc A cắt BC tại M.
a) Chứng minh: △AMB = △AMC.
b) Qua C kẻ đường thẳng song song với AB cắt tia AM tại N. Chứng minh: NC = AB.
c) Chứng minh: AM= 1/2 AN .
a: Xét ΔAMB và ΔAMC có
AM chung
góc MAB=góc MAC
AB=AC
=>ΔAMB=ΔAMC
b: Xét ΔMAB và ΔMNC có
góc AMB=góc NMC
MB=MC
góc ABM=góc NCM
=>ΔMAB=ΔMNC
=>AB=NC
c: ΔMAB=ΔMNC
=>MA=MN
=>AM=1/2AN
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của AB và CD.
a) Chứng minh DN = AM và chứng minh AMND là hình bình hành.
b) Chứng minh MBND là hình bình hành.
c) Chứng minh AN // CM và AN = CM.
d) Chứng minh M, O và N thẳng hàng.
e) Đường chéo BD cắt AN ở I và CM ở Q. Chứng minh BQ = QI = ID.




