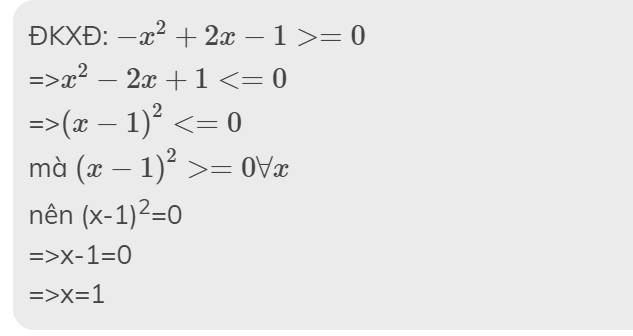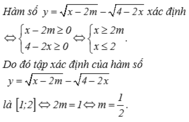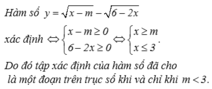căn 8/√x xác định khi và chỉ khi
HT
Những câu hỏi liên quan
Câu 1: Kết quả so sánh 3 và căn 8là: A. 3 sqrt{8} B. 3 sqrt{8} C. 3 ≤ sqrt{8} D. sqrt{3} sqrt{8}Câu 2. sqrt{3x-2} xác định khi và chỉ khi:A. x ≥ 0 B. x ≥ dfrac{2}{3} C. x ≥ dfrac{3}{2} D. x dfrac{2}{3}Câu 3. sqrt{left(1-sqrt{2}right)^2} bằng: A. 3-2sqrt{2} B. 1-sqrt{2} C. sqrt{2}-1 D. 2sqrt{2}+3Câu 4. Kết quả của phép đưa thừa số ra ngoài dấu căn của biểu thức sqrt{a^2b} (với a≥ 0; b ≥ 0) là: ...
Đọc tiếp
Câu 1: Kết quả so sánh 3 và căn 8là:
A. 3 > \(\sqrt{8}\) B. 3 < \(\sqrt{8}\) C. 3 ≤ \(\sqrt{8}\) D. \(\sqrt{3}\)< \(\sqrt{8}\)
Câu 2. \(\sqrt{3x-2}\) xác định khi và chỉ khi:
A. x ≥ 0 B. x ≥ \(\dfrac{2}{3}\) C. x ≥ \(\dfrac{3}{2}\) D. x < \(\dfrac{2}{3}\)
Câu 3. \(\sqrt{\left(1-\sqrt{2}\right)^2}\) bằng:
A. \(3-2\sqrt{2}\) B. \(1-\sqrt{2}\) C. \(\sqrt{2}-1\) D. \(2\sqrt{2}+3\)
Câu 4. Kết quả của phép đưa thừa số ra ngoài dấu căn của biểu thức \(\sqrt{a^2b}\) (với a≥ 0; b ≥ 0) là:
A. \(-b\sqrt{a}\) B. \(b\sqrt{a}\) C .\(a\sqrt{b}\) D. \(-a\sqrt{b}\)
Câu 5. Khử mẫu của biểu thức \(\sqrt{\dfrac{2a}{b}}\) (với a b cùng dấu) ta được:
A. \(\dfrac{\sqrt{2ab}}{a}\) B. \(\dfrac{\sqrt{2ab}}{b}\) C. \(\dfrac{\sqrt{2ab}}{-b}\) D. \(\dfrac{\sqrt{2ab}}{\left|b\right|}\)
Câu 6: Hàm số y = \(\sqrt{5-m}.x+\dfrac{2}{3}\)là hàm số bậc nhất khi:
A. m ≠ 5 B. m > 5 C. m < 5 D. m = 5
Câu 7: Cho 3 đường thẳng (d1) : y = - 2x +1, (d2): y = x + 2, (d3) : y = 1 – 2x. Đường thẳng tạo với trục Ox góc nhọn là:
A. (d1) B. (d2) C. (d3) D. (d1) và (d3)
Câu 8: Hai đường thẳng y = -3x +4 và y = (m+1)x +m song song với nhau khi m bằng:
A. 4 B. -2 C. -3 D. -4
Câu 9. Hàm số bậc nhất nào sau đây nghịch biến?
A. y = \(7+\left(\sqrt{2}-3\right)x\) B. y = \(4-\left(1-\sqrt{3}\right)x\) C. y = \(-5-\left(1-\sqrt{2}\right)x\) D. y = 4+ x
Câu 10. Cặp đường thẳng nào sau đây có vị trí trùng nhau?
A. y=x +2 và y= -x+2 B. y= -3-2x và y= -2x-3
C. y= 2x -1 và y= 2+3x D. y=1 – 2x và y= -2x+3
Câu 11: Đường thẳng có phương trình x + y = 1 cắt đồ thị nào sau đây?
A.y+ x = -1 B. 2x + y = 1 C. 2y = 2 – 2x D. 3y = -3x +1
Câu 12: Cặp số (x; y) nào sau đây là một nghiệm của phương trình 2x – y = 1?
A.(1; -1) B. ( -1; 1) C. (3;2) D. (2; 3)
xác định khi và chỉ khi xác định khi và chỉ khi Enter
Đọc tiếp
xác định khi và chỉ khi xác định khi và chỉ khi Enter

Lời giải:
Phân thức xác định khi và chỉ khi:
\(\left\{\begin{matrix}
x\geq 0\\
x-\sqrt{x}\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\geq 0\\
\sqrt{x}(\sqrt{x}-1)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\geq 0\\
x\neq 0; 1\end{matrix}\right.\)
$\Leftrihgtarrow x>0; x\neq 1$
Đúng 1
Bình luận (0)
Biểu thức x - 4 xác định khi và chỉ khi
A.x > 4
B.x < 4
C.x ≥ 4
D.x ≤ 4
Đáp án là C
Biểu thức x - 4 xác định khi và chỉ khi
x - 4 ≥ 0 ⇔ x ≥ 4
Đúng 0
Bình luận (0)
\(\sqrt{-x^2+2x-1}\) xác định khi và chỉ khi ?
\(\sqrt{-x^2+2x-1}\) xác định khi và chỉ khi ?
ĐKXĐ: \(-x^2+2x-1>=0\)
=>\(x^2-2x+1< =0\)
=>\(\left(x-1\right)^2< =0\)
mà \(\left(x-1\right)^2>=0\forall x\)
nên (x-1)2=0
=>x-1=0
=>x=1
Đúng 0
Bình luận (0)
Biểu thức \(\sqrt{\dfrac{x^2}{x+1}}\) xác định khi và chỉ khi
ĐKXĐ: \(\dfrac{x^2}{x+1}>=0\)
=>x+1>0
=>x>-1
Đúng 0
Bình luận (0)
Tập xác định của hàm số
y
x
-
2
m
-
4
-
2
x
là [1;2] khi và chỉ khi A.
m
-
1
2
B.
m
1
C.
m
1
2
D.
m
1
3
Đọc tiếp
Tập xác định của hàm số y = x - 2 m - 4 - 2 x là [1;2] khi và chỉ khi
A. m = - 1 2
B. m = 1
C. m = 1 2
D. m > 1 3
Tập xác định của hàm số y = x - m - 6 - 2 x là một đoạn trên trục số khi và chỉ khi:
A. m < 3
B. m = 3
C. m > 3
D. m < 1 3
Biểu thức log a b xác định khi và chỉ khi
A. a>0, b>0
B. 0<b#1, a>0
C. 0<a#1, b>0
D. a#1, b>0
\(\sqrt{2x+5}\) xác định khi và chỉ khi.
ĐK: \(2x+5\ge0\Leftrightarrow x\ge-\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
\(2x+5\ge0\Leftrightarrow x\ge\dfrac{-5}{2}\)
Đúng 1
Bình luận (0)
\(\sqrt{2x+5}\) xác định chỉ
khi:\(2x+5\ge0\)
\(\Leftrightarrow x\ge-\dfrac{5}{2}\)
Đúng 0
Bình luận (0)