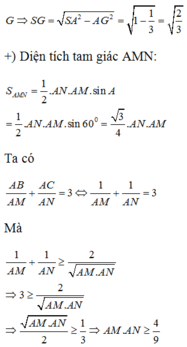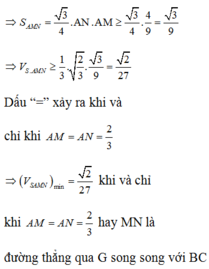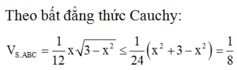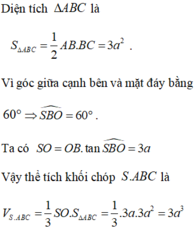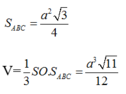Tính thể tích khối tứ diện đều S.ABC có cạnh bằng a
H24
Những câu hỏi liên quan
Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a.
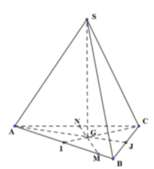
Kẻ SG vuông góc (ABC)
S.ABC là khối chóp đều
=>ΔABC đều
=>G là trọng tâm, là trực tâm của ΔABC
Gọi giao của AG với BC là D
=>D là trung điểm của BC
ΔABC đều có AD là trung tuyến
nên \(AD=\dfrac{a\sqrt{3}}{2}\)
=>\(AG=\dfrac{a\sqrt{3}}{2}\cdot\dfrac{2}{3}=\dfrac{a\sqrt{3}}{3}\)
ΔSAG vuông tại G nên \(SG=\sqrt{SA^2-AG^2}=\sqrt{b^2-\dfrac{1}{3}a^2}\)
\(V_{S.ABC}=\dfrac{1}{3}\cdot S_{ABC}\cdot SG=\dfrac{1}{3}\cdot\sqrt{b^2-\dfrac{1}{3}a^2}\cdot\dfrac{a^2\sqrt{3}}{4}\)
\(=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{\dfrac{3b^2-a^2}{3}}\)
Thể tích khối tứ diện đều có cạnh bằng a là:
\(V=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a^3\sqrt{2}}{12}\)
Đúng 0
Bình luận (0)
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất
V
m
i
n
của khối tứ diện SAMN. A.
V
min
2
27
B.
V
min
4
9...
Đọc tiếp
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất V m i n của khối tứ diện SAMN.
A. V min = 2 27
B. V min = 4 9
C. V min = 2 18
D. V min = 2 36
Chọn A.
Phương pháp:
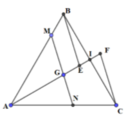
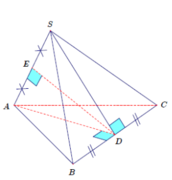
Cho tam giác đều ABC, G là trọng tâm tam giác ABC. Đường thẳng qua G cắt AB, AC lần lượt tại M, N. Khi đó, 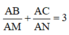
Thật vậy, gọi I là trung điểm của BC, qua B, C kẻ các đường thẳng song song MN, cắt đường thẳng AI tại E, F.

Cách giải:
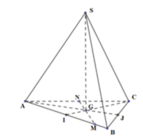
Do SABC là tứ diện đều, G là trọng tâm tam giác ABC

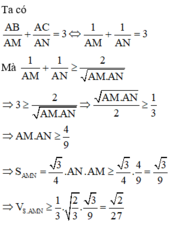

Đúng 0
Bình luận (0)
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất Vmin của khối tứ diện SAMN.
Đọc tiếp
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất Vmin của khối tứ diện SAMN.
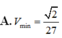
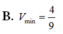
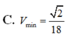
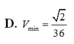
Cho tứ diện S.ABC có cạnh SA và tất cả các cạnh còn lại đều bằng 1. Tìm giá trị lớn nhất thể tích tứ diện S.ABC?
Đọc tiếp
Cho tứ diện S.ABC có cạnh SA và tất cả các cạnh còn lại đều bằng 1. Tìm giá trị lớn nhất thể tích tứ diện S.ABC?
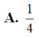
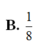
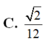
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng
2
k
3
12
. Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng
a
2
. Tính theo a thể tích khối tứ diện
A
C
B
D...
Đọc tiếp
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng 2 k 3 12 . Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a 2 . Tính theo a thể tích khối tứ diện A C B ' D ' .
A. 2 2 a 3 3
B. 2 a 3 6
C. 2 a 3 2
D. a 3 3
Chọn đáp án A.

Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:
1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng
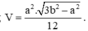
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là ![]()
3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là
![]()
4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là
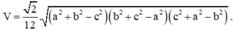
Đúng 0
Bình luận (0)
Chóp tam giác đều S.ABC có đáy là tam giác đều với diện tích bằng
3
a
2
3
4
. Biết rằng độ dài cạnh bên bằng
a
7
. Tính thể tích khối chóp S.ABC.
Đọc tiếp
Chóp tam giác đều S.ABC có đáy là tam giác đều với diện tích bằng 3 a 2 3 4 . Biết rằng độ dài cạnh bên bằng a 7 . Tính thể tích khối chóp S.ABC.
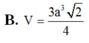
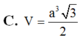
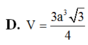
Cho khối chóp đều S.ABC có cạnh đáy bằng a. Tính thể tích khối chóp S.ABC biết cạnh bên bằng a. A.
V
S
.
ABC
a
3
2
12
B.
V
S
.
ABC
a
3...
Đọc tiếp
Cho khối chóp đều S.ABC có cạnh đáy bằng a. Tính thể tích khối chóp S.ABC biết cạnh bên bằng a.
A. V S . ABC = a 3 2 12
B. V S . ABC = a 3 3 6
C. V S . ABC = a 3 12
D. V S . ABC = a 3 4
Đáp án A
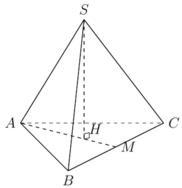
Gọi H là tâm của tam giác đều ABC. Gọi M là trung điểm của BC.
Vì tam giác ABC đều cạnh a nên:
A M = a 3 2 và A H = 2 3 A M = a 3 3
Tam giác SAH vuông tại H
⇒ S H = S A 2 - A H 2 = a 2 - a 2 3 = a 6 3
Thể tích khối chóp S.ABC là:
V = 1 3 . S A B C . S H = 1 3 . a 2 3 4 . a 6 3 = a 3 2 12
Đúng 0
Bình luận (0)
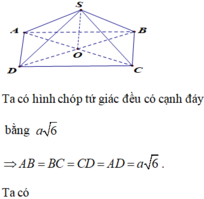
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
a
6
, góc giữa cạnh bên và mặt đáy bằng
60
0
. Tính thể tích V của khối chóp S.ABC? A.
V
9
a
3
B.
V
2
a
3
C.
V
3
a
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 6 , góc giữa cạnh bên và mặt đáy bằng 60 0 . Tính thể tích V của khối chóp S.ABC?
A. V = 9 a 3
B. V = 2 a 3
C. V = 3 a 3
D. V = 6 a 3
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a . Tính thể tích V của khối chop S.ABC
Đọc tiếp
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a . Tính thể tích V của khối chop S.ABC
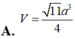
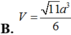
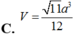

Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 3a. Thể tích khối chóp S.ABC tính theo a là: A.
26
a
3
12
B.
78
a
3
12
C.
26...
Đọc tiếp
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 3a. Thể tích khối chóp S.ABC tính theo a là:
A. 26 a 3 12
B. 78 a 3 12
C. 26 a 3 3
D. 78 a 3 3
Đáp án A
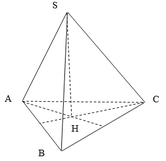
Gọi H là hình chiếu của S lên (ABCD)
Ta có: A H = a 2 − a 2 2 = a 3 3 ;
S H = 3 a 2 − a 3 3 2 = 26 3 a
Thể tích khối chóp là:
V = 1 3 S H . S A B C D = 1 3 . 26 3 a . 1 2 a 2 sin 60 ° = 26 a 3 12
Đúng 0
Bình luận (0)