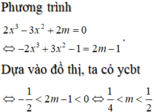1/ Vẽ đồ thị hàm số (P):y=3x2

Những câu hỏi liên quan
Cho hàm số
y
f
x
x
3
−
3
x
2
+
2
có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số
y
f
x
+
1
? A. B. C. D.
Đọc tiếp
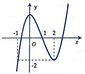
Cho hàm số y = f x = x 3 − 3 x 2 + 2 có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số y = f x + 1 ?
A. 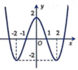
B. 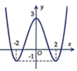
C. 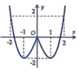
D. 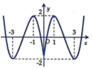
Cho hàm số
y
f
(
x
)
x
3
-
3
x
2
+
2
có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số
y
x
+
1
? A. B. C. D.
Đọc tiếp
Cho hàm số y = f ( x ) = x 3 - 3 x 2 + 2 có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số y = x + 1 ?
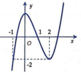
A. 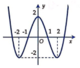
B. 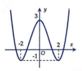
C. 
D. 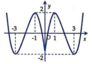
Đáp án C.
Tịnh tiến đồ thị hàm số y = f x sang trái 1 đơn vị.
Giữ nguyên phần đồ thị hàm số nằm bên phải trục tung. Xóa phần đồ thị hàm số nằm bên trái trục tung.
Lấy đối xứng phần đồ thị hàm số nằm bên phải trục tung qua trục tung.
Từ đây ta có đồ thị hàm số y = f x + 1 .
Đúng 0
Bình luận (0)
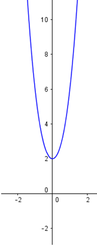
Với giá trị nào của m thì đồ thị hàm số
y
x
3
+
3
x
2
+
m
+
2
cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số
y
x
3
+
3
x
2
+
2
được cho như hình vẽ. A.
m
2
B. ...
Đọc tiếp
Với giá trị nào của m thì đồ thị hàm số y = x 3 + 3 x 2 + m + 2 cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số y = x 3 + 3 x 2 + 2 được cho như hình vẽ.
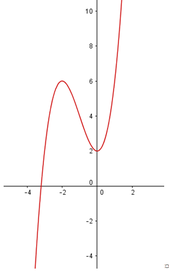
A. m > 2
B. m < 2
C. Không có giá trị nào của m thỏa mãn
D. m ≥ 2
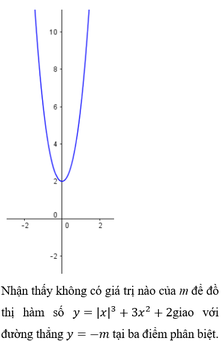
Với giá trị nào của m thì đồ thị hàm số
y
|
x
3
|
+
3
x
2
+
m
+
2
cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số
y
x...
Đọc tiếp
Với giá trị nào của m thì đồ thị hàm số y = | x 3 | + 3 x 2 + m + 2 cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số y = x 3 + 3 x 2 + 2 được cho như hình vẽ .
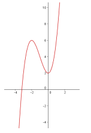
A. m > 2
B. m ≥ 2
C. m < 2
D. Không có giá trị nào của m thỏa mãn
Cho hàm số
y
-
x
3
+
3
x
2
-
2
có đồ thị như hình vẽ: Số nghiệm của phương trình
x
3
-
3
x
2
+
2...
Đọc tiếp
Cho hàm số y = - x 3 + 3 x 2 - 2 có đồ thị như hình vẽ:
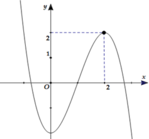
Số nghiệm của phương trình x 3 - 3 x 2 + 2 = 1 là
A. 3
B. 4
C. 6
D. 5
Cho hàm số
y
-
2
x
3
+
3
x
2
-
1
có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình
2
x
3
-
3
x
2
+
2
m
có đúng 3 nghiệm phân biệt, tron...
Đọc tiếp
Cho hàm số y = - 2 x 3 + 3 x 2 - 1 có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình 2 x 3 - 3 x 2 + 2 m có đúng 3 nghiệm phân biệt, trong đó có 2 nghiệm lớn hơn 1 2
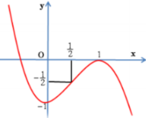
A. m ∈ - 1 2 ; 0
B. m ∈ - 1 ; 0
C. m ∈ 0 ; 1 2
D. m ∈ 1 4 ; 1 2
Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x 3 + 3 x 2 + 1

+ Bảng biến thiên:
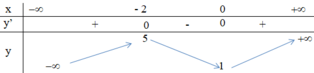
Kết luận:
Hàm số đồng biến trên các khoảng (-∞; -2) và (0; +∞).
Hàm số nghịch biến trên khoảng (-2; 0).
Hàm số đạt cực tiểu tại x = 0 ; y C T = 1 .
Hàm số đạt cực đại tại x = -2 ; y C Đ = 5 .
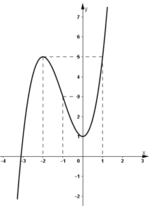
- Đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (–3; 1), (1; 5).
Đúng 0
Bình luận (0)
Đồ thị của hàm số y
-
x
3
+
3
x
2
+
2
x
-
1
và đồ thị hàm số
y
3
x
2
-
3
x
-
1
có tất cả bao nhiêu điểm chung? A. 0 B. 2 C. 3 D. 1
Đọc tiếp
Đồ thị của hàm số y = - x 3 + 3 x 2 + 2 x - 1 và đồ thị hàm số y = 3 x 2 - 3 x - 1 có tất cả bao nhiêu điểm chung?
A. 0
B. 2
C. 3
D. 1
Đồ thị của hàm số
y
−
x
3
+
3
x
2
+
2
x
−
1
và đồ thị hàm số
y
3
x
2
−
2
x
−
1
có tất cả bao nhiêu điểm chung? A. 0 B. 2 C. 3 D. 1
Đọc tiếp
Đồ thị của hàm số y = − x 3 + 3 x 2 + 2 x − 1 và đồ thị hàm số y = 3 x 2 − 2 x − 1 có tất cả bao nhiêu điểm chung?
A. 0
B. 2
C. 3
D. 1
Đáp án là C
• Phương trình hoành độ giao điểm của hai đồ thị:
Đúng 0
Bình luận (0)
a) Vẽ đồ thị hàm số y = 3x2
b) Biết đồ thị hàm số đã cho cắt đường thẳng y = 2x + 2. Tìm tọa độ giao điểm của chúng?
a, Đồ thị hàm số \(y=3x^2\)
b, Phương trình hoành độ giao điểm của đường thẳng \(y=2x+2\) và parabol \(y=3x^2\) là: \(3x^2=2x+2\Leftrightarrow x=\dfrac{1\pm\sqrt{7}}{3}\)
Với \(x=\dfrac{1+\sqrt{7}}{3}\Rightarrow y=\dfrac{8+2\sqrt{7}}{3}\Rightarrow\left(\dfrac{1+\sqrt{7}}{3};\dfrac{8+2\sqrt{7}}{3}\right)\)
Với \(x=\dfrac{1-\sqrt{7}}{3}\Rightarrow y=\dfrac{8-2\sqrt{7}}{3}\Rightarrow\left(\dfrac{1-\sqrt{7}}{3};\dfrac{8-2\sqrt{7}}{3}\right)\)
Đúng 2
Bình luận (2)
Sửa đề: \(y=2x+1\)
b) Phương trình hoành độ giao điểm là:
\(3x^2=2x+1\)
\(\Leftrightarrow3x^2-2x-1=0\)
a=3; b=-2; c=-1
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{-1}{3}\)
Thay x=1 vào y=2x+1, ta được:
\(y=2\cdot1+1=3\)
Thay \(x=-\dfrac{1}{3}\) vào y=2x+1, ta được:
\(y=2\cdot\dfrac{-1}{3}+1=\dfrac{-2}{3}+1=\dfrac{1}{3}\)
Vậy: Tọa độ giao điểm là (1;3) và \(\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\)
Đúng 1
Bình luận (2)