Giải giúp c bài 8,9,10 ạ
BT
Những câu hỏi liên quan
giúp 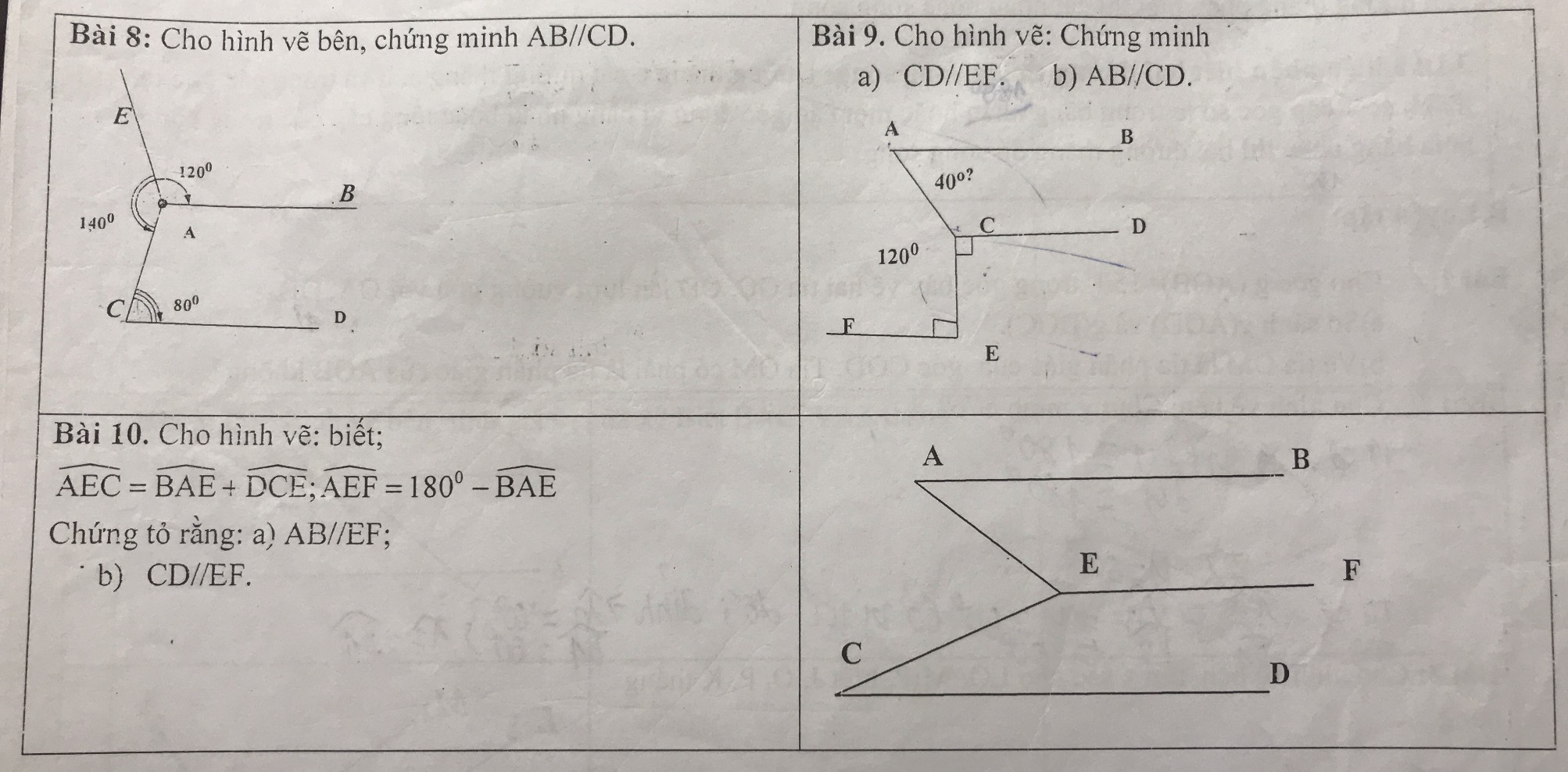 em bài 8,9,10 với ạ
em bài 8,9,10 với ạ
em cam ơn nhiều
giúp em với ạ em cảm ơn nhiều chứ em mệt lắm ùi ui![]()
Đúng 0
Bình luận (0)
Giúp mình câu 8,9,10 với ạ
Câu 8:
a, Giả sử: \(\left\{{}\begin{matrix}n_{CaCO_3}=x\left(mol\right)\\n_{MgCO_3}=y\left(mol\right)\end{matrix}\right.\)
⇒ 100x + 84y = 46,8 (1)
Theo PT: \(\left\{{}\begin{matrix}n_{CaO}=n_{CaCO_3}=x\left(mol\right)\\n_{MgO}=n_{MgCO_3}=y\left(mol\right)\end{matrix}\right.\)
⇒ 56x + 40y = 24,8 (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=0,3\left(mol\right)\\y=0,2\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CaCO_3}=\dfrac{0,3.100}{46,8}.100\%\approx64,1\%\\\%m_{MgCO_3}\approx35,9\%\end{matrix}\right.\)
b, Theo PT: \(n_{CO_2}=0,3+0,2=0,5\left(mol\right)\)
\(\Rightarrow V_{CO_2}=0,5.22,4=11,2\left(l\right)\)
Bạn tham khảo nhé!
Đúng 2
Bình luận (0)
Câu 9:
Giả sử KL cần tìm là A.
PT: \(A+2HCl\rightarrow ACl_2+H_2\)
Theo PT: \(n_A=n_{ACl_2}\)
\(\Rightarrow\dfrac{4,8}{M_A}=\dfrac{19}{M_A+71}\) \(\Rightarrow M_A=24\left(g/mol\right)\)
Vậy: A là Mg.
Bạn tham khảo nhé!
Đúng 2
Bình luận (0)
Câu 10:
a, Ta có: nHCl = 0,4.0,2 = 0,08 (mol)
Theo PT: \(n_{CaCO_3}=n_{CO_2}=\dfrac{1}{2}n_{HCl}=0,04\left(mol\right)\)
\(\Rightarrow m_{CaCO_3}=0,04.100=4\left(g\right)\)
\(V_{CO_2}=0,04.22,4=0,896\left(l\right)\)
b, Theo PT: \(n_{CaCl_2}=\dfrac{1}{2}n_{HCl}=0,04\left(mol\right)\)
\(\Rightarrow C_{M_{CaCl_2}}=\dfrac{0,04}{0,2}=0,1M\)
Bạn tham khảo nhé!
Đúng 2
Bình luận (0)
Mik cần giúp câu 8,9,10 ạ
8 arrives
9 isn't using
10 does - start
Bài 3
1 won't
2 will
3 won't
4 will
5 will
6 won't
7 will
8 won't
9 will
10 will
Đúng 2
Bình luận (0)
Mik cần giúp câu 8,9,10 vs ạ 
Bạn chụp đề rõ ràng ra nha, thiếu vế sau
Đúng 1
Bình luận (0)
làm hộ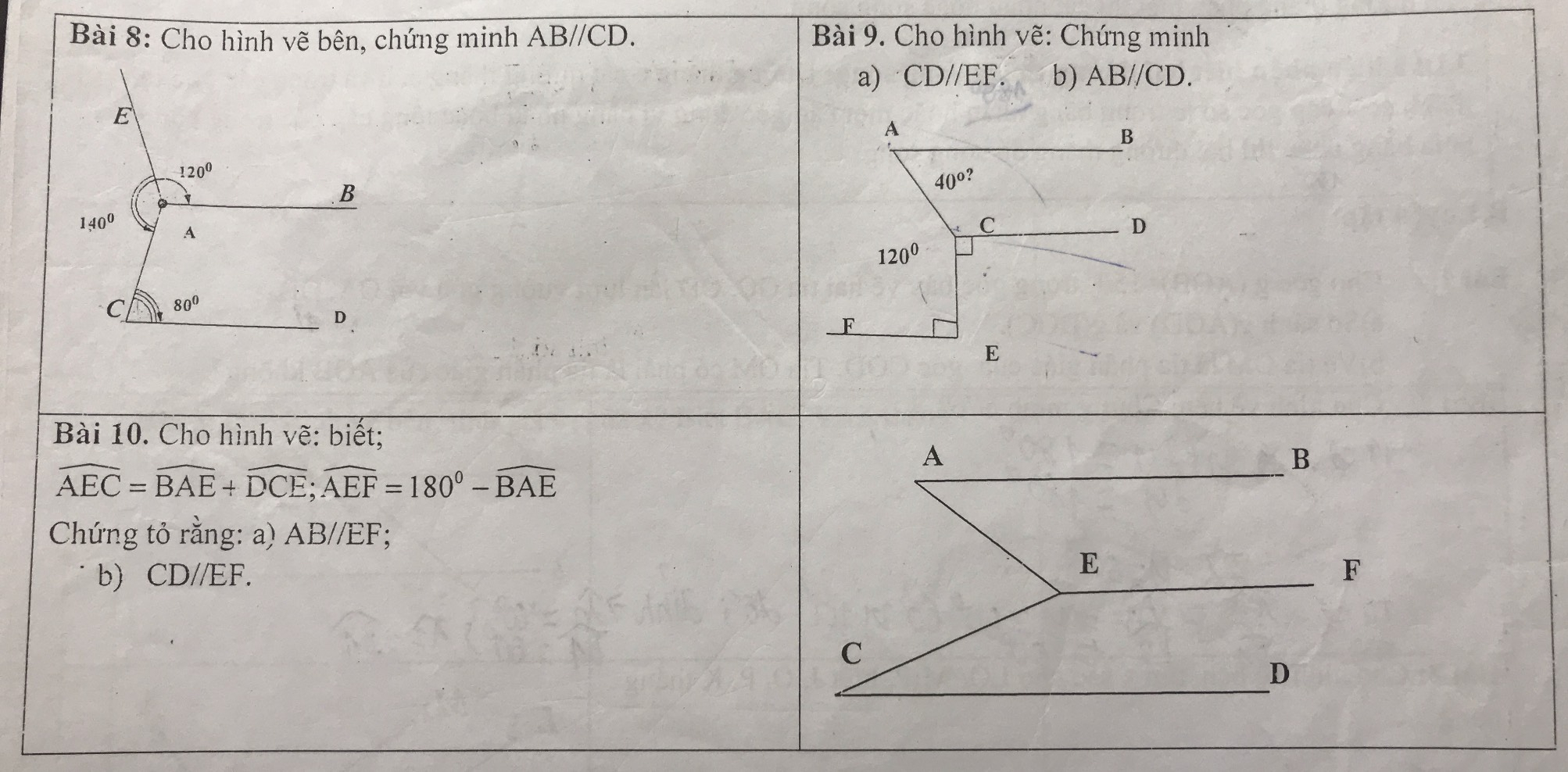 em bài 8,9,10 với ạ em gấp lắm rùi
em bài 8,9,10 với ạ em gấp lắm rùi
em cảm ơn nhiều
Bài này mik giả cho người khác rồi, bn bấm tìm đề là ra
Đúng 0
Bình luận (0)
https://hoc24.vn/cau-hoi/.1685893843618 (hoặc bn vào link này cho nhanh cũng đc, mik giải rồi)
Đúng 0
Bình luận (0)
Bài 10 thì mik chưa làm dc, bn thông cảm
Đúng 0
Bình luận (0)
Giải giúp mình bài này với ạ giải câu c chi tiết xíu giúp mình với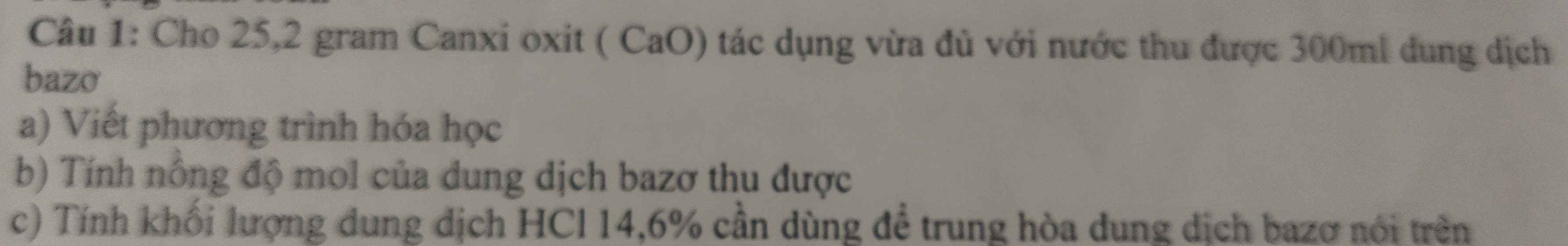
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Đúng 1
Bình luận (1)
BÀI 8,9,10 BÀI 3 TO
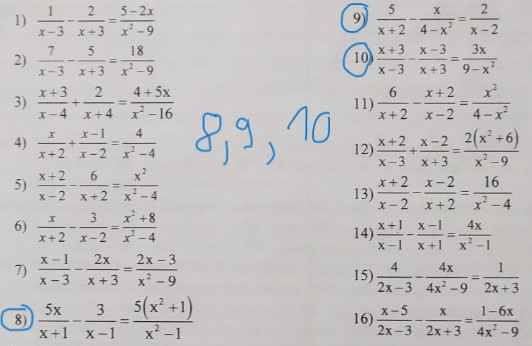 Giup mình bài 8,9,10
Giup mình bài 8,9,10
8: =>5x(x-1)-3(x+1)=5x^2+5
=>5x^2-5x-3x-3=5x^2+5
=>-8x=8
=>x=-1(loại)
9: =>5(x-2)+x=2(x+2)
=>5x-10+x=2x+4
=>6x-10=2x+4
=>4x=14
=>x=3,5(nhận)
10: =>(x+3)^2-(x-3)^2=-3x
=>x^2+6x+9-x^2+6x-9=-3x
=>12x+3x=0
=>x=0
Đúng 0
Bình luận (0)
\(8,\dfrac{5x}{x+1}-\dfrac{3}{x-1}=\dfrac{5\left(x^2+1\right)}{x^2-1}\left(dkxd:x\ne\pm1\right)\)
\(\Leftrightarrow\dfrac{5x}{x+1}-\dfrac{3}{x-1}-\dfrac{5\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow5x\left(x-1\right)-3\left(x+1\right)-5x^2-5=0\)
\(\Leftrightarrow5x^2-5x-3x-3-5x^2-5=0\)
\(\Leftrightarrow-8x-8=0\)
\(\Leftrightarrow-8\left(x+1\right)=0\)
\(\Leftrightarrow x=-1\left(ktmdk\right)\)
Vậy \(S=\varnothing\)
\(9,\dfrac{5}{x+2}-\dfrac{4}{4-x^2}=\dfrac{2}{x-2}\)
\(\Leftrightarrow\dfrac{5}{x+2}-\dfrac{4}{x^2-4}-\dfrac{2}{x-2}=0\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow5\left(x-2\right)-4-2\left(x+2\right)=0\)
\(\Leftrightarrow5x-10-4-2x-4=0\)
\(\Leftrightarrow3x-18=0\)
\(\Leftrightarrow3x=18\)
\(\Leftrightarrow x=6\left(tmdk\right)\)
Vậy \(S=\left\{6\right\}\)
Đúng 0
Bình luận (0)





