8: =>5x(x-1)-3(x+1)=5x^2+5
=>5x^2-5x-3x-3=5x^2+5
=>-8x=8
=>x=-1(loại)
9: =>5(x-2)+x=2(x+2)
=>5x-10+x=2x+4
=>6x-10=2x+4
=>4x=14
=>x=3,5(nhận)
10: =>(x+3)^2-(x-3)^2=-3x
=>x^2+6x+9-x^2+6x-9=-3x
=>12x+3x=0
=>x=0
\(8,\dfrac{5x}{x+1}-\dfrac{3}{x-1}=\dfrac{5\left(x^2+1\right)}{x^2-1}\left(dkxd:x\ne\pm1\right)\)
\(\Leftrightarrow\dfrac{5x}{x+1}-\dfrac{3}{x-1}-\dfrac{5\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow5x\left(x-1\right)-3\left(x+1\right)-5x^2-5=0\)
\(\Leftrightarrow5x^2-5x-3x-3-5x^2-5=0\)
\(\Leftrightarrow-8x-8=0\)
\(\Leftrightarrow-8\left(x+1\right)=0\)
\(\Leftrightarrow x=-1\left(ktmdk\right)\)
Vậy \(S=\varnothing\)
\(9,\dfrac{5}{x+2}-\dfrac{4}{4-x^2}=\dfrac{2}{x-2}\)
\(\Leftrightarrow\dfrac{5}{x+2}-\dfrac{4}{x^2-4}-\dfrac{2}{x-2}=0\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow5\left(x-2\right)-4-2\left(x+2\right)=0\)
\(\Leftrightarrow5x-10-4-2x-4=0\)
\(\Leftrightarrow3x-18=0\)
\(\Leftrightarrow3x=18\)
\(\Leftrightarrow x=6\left(tmdk\right)\)
Vậy \(S=\left\{6\right\}\)

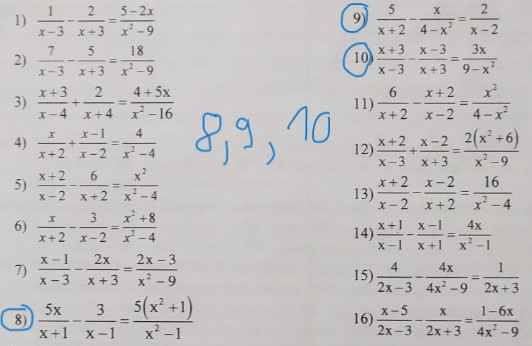 Giup mình bài 8,9,10
Giup mình bài 8,9,10





