Tìm tất cả các số thực a sao cho đa thức x4 + x3 -2x2 + x + a chia hết cho đa thức x + 1
NK
Những câu hỏi liên quan
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)
Bài 5: Tìm a, b sao cho
a/ Đa thức x4 – x3 + 6x2 – x + a chia hết cho đa thức x2 – x + 5
b/ Đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
Đặt \(f\left(x\right)=2x^3-3x^2+x+a\)
Ta có: phép chia \(f\left(x\right)\) cho \(x+2\) có dư là \(R=f\left(-2\right)\)
\(\Rightarrow f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a\)
\(f\left(-2\right)=2.\left(-8\right)-3.4-2+a\)
\(f\left(-2\right)=-16-12-2+a\)
\(f\left(-2\right)=-20+a\)
Để \(f\left(x\right)\) chia hết cho \(x+2\) thì \(R=0\) hay \(f\left(-2\right)=0\)
\(\Rightarrow-20+a=0\Leftrightarrow a=20\)
Đúng 0
Bình luận (0)
Cho đa thức A = x4 + x3 – 2x – 2
a) Tìm đa thức B sao cho A + B = x3 + 3x + 1
b) Tìm đa thức C sao cho A – C = x5
c) Tìm đa thức D biết rằng D = (2x2 – 3) . A
d) Tìm đa thức P sao cho A = (x+1) . P
e) Có hay không một đa thức Q sao cho A = (x2 + 1) . Q?
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
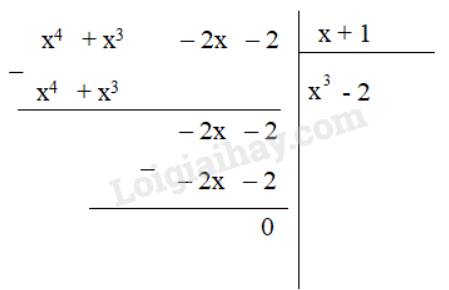
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
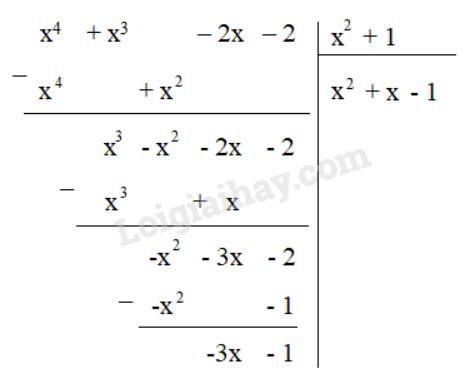
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
Đúng 1
Bình luận (0)
a) Thực hiện phép chia đa thức (2x4 - 6x3 +12x2 - 14x + 3) cho đa thức (x2 – 4x +1)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
Đúng 3
Bình luận (0)
Bài 1 : Tìm a để (5x3 - 3x2 + 2x +a) chia hết cho ( x +1)Bài 2 : Tìm a để phép chia sau là phép chia hết :a) ( x3 - x2 + 2x + a) chia hết cho x -1b) x3 -2x2 -2x + a chia hết cho x +1Bài 3 Tìm các giá trị a , b ,k để đa thức f(x) chia hết cho đa thức g(x)a) f(x) x4 -9x3 + 21x2 + x +k ; g (x) x2 - x -2b) f(x) x4 - 3x3 + 3x2 + ax + b ; g(x) x2 - 3x +4
Đọc tiếp
Bài 1 : Tìm a để (5x3 - 3x2 + 2x +a) chia hết cho ( x +1)
Bài 2 : Tìm a để phép chia sau là phép chia hết :
a) ( x3 - x2 + 2x + a) chia hết cho x -1
b) x3 -2x2 -2x + a chia hết cho x +1
Bài 3 Tìm các giá trị a , b ,k để đa thức f(x) chia hết cho đa thức g(x)
a) f(x)= x4 -9x3 + 21x2 + x +k ; g (x) = x2 - x -2
b) f(x) = x4 - 3x3 + 3x2 + ax + b ; g(x) = x2 - 3x +4
Bài 1:
Ta có: \(5x^3-3x^2+2x+a⋮x+1\)
\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)
\(\Leftrightarrow a-10=0\)
hay a=10
Đúng 0
Bình luận (0)
a/ Tìm a sao cho đa thức : x4 – x3 + 6x2 – x + a chia hết cho đa thức: x2 – x + 5
b/ Tính giá trị nguyên của n để giá trị của biểu thức : 3n3 + 10n2 – 5 chia hết cho giá trị của biểu thức: 3n + 1
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
Đúng 1
Bình luận (0)
Cho đa thức A 5 x2y + xy – xy2 - x2y + 2xy + x2y + xy + 6. Thu gọn rồi xác định bậc của đa thức.a/ Tìm đa thức B sao cho A + B 0b/ Tìm đa thức C sao cho A + C -2xy + 1 Bài 6: Cho đa thức F(x) 2x3 – x5 + 3x4 + x2 - x3 + 3x5 – 2x2 - x4 + 1
Đọc tiếp
Cho đa thức A = 5 x2y + xy – xy2 - ![]() x2y + 2xy + x2y + xy + 6. Thu gọn rồi xác định bậc của đa thức.
x2y + 2xy + x2y + xy + 6. Thu gọn rồi xác định bậc của đa thức.
a/ Tìm đa thức B sao cho A + B = 0
b/ Tìm đa thức C sao cho A + C = -2xy + 1
Bài 6: Cho đa thức F(x) = 2x3 – x5 + 3x4 + x2 - ![]() x3 + 3x5 – 2x2 - x4 + 1
x3 + 3x5 – 2x2 - x4 + 1
\(A=5x^2y-xy^2+4xy+6\) bậc : 3
a)\(B=-5x^2y+xy^2-4xy-6\)
b)\(=>C=-2xy+1-5x^2y+xy^2-4xy-6\)
\(C=-5x^2y+xy^2-6xy-5\)
Đúng 1
Bình luận (1)
Tìm a để đa thức x 4 - x 3 + 6 x 2 - x + a chia hết cho đa thức x 2 - x + 5
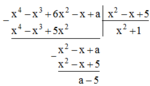
Để có phép chia hết thì số dư phải bằng 0.
Ta có: a – 5 = 0 hay a = 5.
Đúng 0
Bình luận (0)




