giải phương trình bài này với ạ
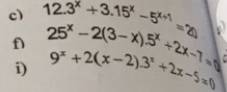
 mọi ng giải hộ em bài này với ạ( có lập bảng và giải bằng hệ phương trình ạ) e cần gấp
mọi ng giải hộ em bài này với ạ( có lập bảng và giải bằng hệ phương trình ạ) e cần gấp
Ai giúp e bài này với ạ: Giải phương trình( giải giúp e câu 3 và câu 4 phần này với ạ)

Câu 3 và caau4 bài giải phương trình nhé
Bài 3. Đặt ẩn phụ là
\(a=2x-\frac{5}{x}\\\)
\(b=x-\frac{1}{x}\)
pt <=> \(b-a=\sqrt{a}-\sqrt{b}\\ \)
\(\left(\sqrt{b}-\sqrt{a}\right)\left(\sqrt{b}+\sqrt{a}\right)=-\left(\sqrt{b}-\sqrt{a}\right)\\ \)
\(\left(\sqrt{b}-\sqrt{a}\right)\left(\sqrt{b}+\sqrt{a}+1\right)=0\)
tới đây xét 2 TH bạn tự giải nhé
Với những dạng bài giải phương trình/bất phương trình mà có kết quả như thế này thì kết luận sao ạ?
\(0=0\) (luôn đúng)
\(-1>0\) (vô lí)
0=0 thì pt thoả mãn với mọi x
-1>0 pt vô nghiệm \(S=\varnothing\)
`1.` Với `0=0(` luôn đúng `)` `->` Kết luận: Vậy `S={x|x\inRR}`
`2.` Với `-1>0(` vô lý `)` `->` Kết luận: Vậy `S=∅`
giải bất phương trình
\(\dfrac{x-3}{2+x}\)<1
giúp em với ạ còn đúng bài này chưa biết làm
\(\dfrac{x-3}{2+x}< 1\\ \Leftrightarrow\dfrac{x-3}{2+x}-1< 0\\ \Leftrightarrow\dfrac{x-3}{2+x}-\dfrac{2+x}{2+x}< 0\\ \Leftrightarrow\dfrac{x-3-2-x}{2+x}< 0\\ \Leftrightarrow\dfrac{-5}{2+x}< 0\)
Vì \(-5< 0\)
\(\Rightarrow2+x>0\\ \Rightarrow x>-2\)
Vậy \(x>-2\)
Giải hộ em phương trình này với ạ đang làm bài cái lú ngang :(( (x-1)³ +x³ +(x+1)³=(x +2 )³
\(\left(x-1\right)^3+x^3+\left(x+1\right)^3=\left(x+2\right)^3\)
\(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1-x^3-6x^2-12x-8=0\)
\(\Leftrightarrow2x^3-6x^2-6x-8=0\)
\(\Leftrightarrow2.\left(x^3-3x^2-3x-4\right)=0\)
\(\Leftrightarrow x^3-4x^2+x^2-4x+x-4=0\)
\(\Leftrightarrow x^2.\left(x-4\right)+x.\left(x-4\right)+\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right).\left(x^2+x+1\right)=0\)
Mà \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
\(\Rightarrow x-4=0\Leftrightarrow x=4\)
* mọi người giúp mình 2 bài này với ạ*
Bài 8: Cho phương trình (a2 - 4)x -12x + 7 = 0 (a là tham số)
a) Giải phương trình với a = 1
b) Tìm các giá trị của a sao cho phương trình nhận x = 1 là nghiệm.
c) Tìm điều kiện của a để phương trình đã cho luôn có một nghiệm duy nhất
Bài 9: Giải và biện luận phương trình ẩn x theo tham số m
a) (m2 - 9)x - m + 3 = 0
b)\(\dfrac{x+3}{x-1}=\dfrac{x+m}{x+1}\)
Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)
Bài 2 Cho phương trình x2-2(m+1) x+2m+1=0
A) Tìm m để phương trình có hai nghiệm trái dấu
B ) Tìm m để phương trình có hai nghiệm nằm cùng phía với trục Oy
Ai giải hộ mình bài này được ko ạ
a.
Phương trình có 2 nghiệm trái dấu khi và chỉ khi:
\(ac< 0\Leftrightarrow1.\left(2m+1\right)< 0\)
\(\Leftrightarrow m< -\dfrac{1}{2}\)
b.
Phương trình có 2 nghiệm nằm cùng phía trục Oy \(\Leftrightarrow\) phương trình có 2 nghiệm cùng dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m+1\right)^2-\left(2m+1\right)>0\\x_1x_2=2m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m>-\dfrac{1}{2}\end{matrix}\right.\)
Mọi người chỉ mình ạ!
Bài 1: giải phương trình
\(\sqrt{5x^2}=2x-1\)
* Chỉ mình tại sao bài này nếu mà bình phương 2 vế lên có giải được ra kết quả đúng không ạ. Giair thích rõ và chi tiết giúp mình nhé
* Với nhưng dạng thế nào thì có thể bình phương ạ!
Bài 2: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
* Với bài này mình chưa tìm điều kiện luôn mà giải ra thành \(\sqrt{x+1}=1\) rồi tìm điều kiện \(x+1\ge0\) cũng được ạ các bạn.
* Nó có phụ thuộc vào dạng bài không ạ hay là chỉ có những bài mới được làm như vậy còn chỉ có những bài thì phải tìm điều kiện ngay từ đầu ạ ( và làm như vậy có bị mất trường hợp nào đi không) . giải thích tại sao
Bài 3:
Ví dụ: \(x^2\ge2x\) .
* Tại sao khi mà chia cả hai vế cho x thì chỉ nhân 1 trường hợp ( bị thiếu trường hợp). Còn khi mà chuyển vế sang cho lớn hơn hoặc bằng 0 thì lại đủ trường hợp. giải thích mình tại sao lại bị thiếu và đủ trường hợp ạ!
Giups mình đầy đủ chỗ (*) nhá!
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
Bài 2: ĐKXĐ luôn là thứ mà phải ghi ngay đầu bài làm để xác định được biểu thức có nghĩa. Tức là em ghi ĐKXĐ: $x+1\geq 0$ đầu tiên.
Sau đó mới giải ra $\sqrt{x+1}=1$
`2x+5y=11(1)`
`2x-3y=0(2)`
Lấy (1) trừ (2)
`=>8y=11`
`<=>y=11/8`
`<=>x=(3y)/2=33/16`
a) Ta có: \(\left\{{}\begin{matrix}2x+5y=11\\2x-3y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=11\\2x-3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{11}{8}\\2x=3y=3\cdot\dfrac{11}{8}=\dfrac{33}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{33}{16}\\y=\dfrac{11}{8}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{33}{16}\\y=\dfrac{11}{8}\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}4x+3y=6\\2x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\4x+2y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\2x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-2=4\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=6\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(3;-2)
`b)4x+3y=6(1)`
`2x+y=4<=>4x+2y=8(2)`
Lấy (1) trừ (2) ta có:
`y=-2`
`<=>x=(4-2y)/2=3`