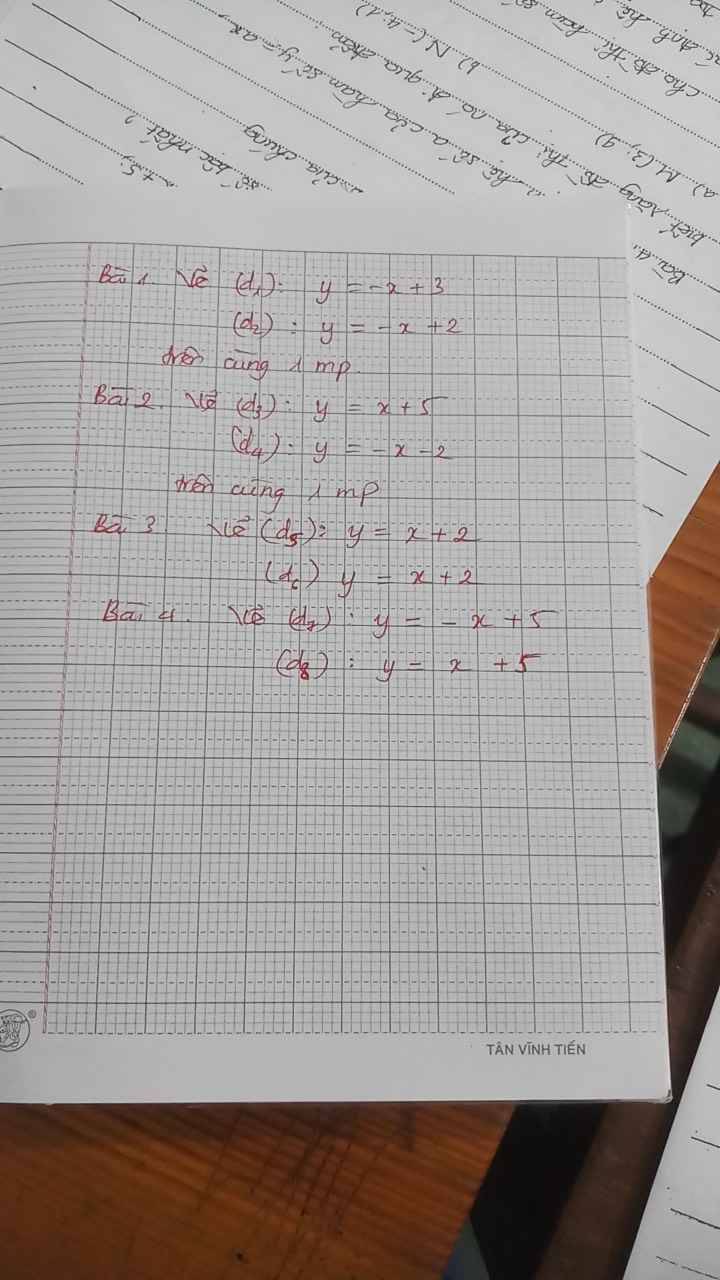
giúp mình với ạaaaaa
 giúp mình câu 2 với ạaaaaa
giúp mình câu 2 với ạaaaaa
Câu 2:
=>x=1-y và m(1-y)-y=2m
=>x=1-y và m-my-y=2m
=>x=1-y và y(-m-1)=m
=>x=1-y và y=-m/m+1
=>x=1+m/m+1=(m+2)/m+1 và y=-m/m+1
Để x,y nguyên thì m+1+1 chia hết cho m+1 và -m-1+1 chia hết cho m+1
=>\(m+1\in\left\{1;-1\right\}\)
mà m<>0
nên m=-2
Giúp mình bìa 7 ,8 với ạaaaaa 
GIÚP EM VỚI ẠAAAAA


giúp emmmm với ạaaaaa
45. I know how to use this machine, I can help you.
46. excited about the journey.
47. Peter is the best student in my class who can solve this difficult problem.
48. very good at typing.
GIÚP EM VỚI ẠAAAAA
Ta có: \(x^2-3x+2=\left(1-x\right)\sqrt{3x-2}\) \(\left(x\ge\dfrac{2}{3}\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-\left(1-x\right)\sqrt{3x-2}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2+\sqrt{3x-2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(TM\right)\\\sqrt{3x-2}=2-x\left(1\right)\end{matrix}\right.\)
Xét (1) ta có: \(\left\{{}\begin{matrix}2-x\ge0\\3x-2=4-4x+x^2\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}2\ge x\\x^2-7x+6=0\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x\le2\\\left[{}\begin{matrix}x=6\left(KTM\right)\\x=1\left(TM\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy nghiệm của phương trình là x=1
ĐKXĐ : x \(\ge\dfrac{2}{3}\)
Ta có \(\left(x-1\right)\left(x-2\right)=\sqrt{3x-2}\left(1-x\right)\)
<=> \(\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\sqrt{3x-2}=2-x\end{matrix}\right.\)
Khi x - 1 = 0 <=> x = 1 (tm)
Khi \(\sqrt{3x-2}=2-x\)
<=> \(\left\{{}\begin{matrix}3x-2=x^2-4x+4\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-7x+6=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-6\right)=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow x=1\)
Vậy phương trình 1 nghiêm \(x=1\)
\(ĐK:x\ge\dfrac{2}{3}\)
\(\Leftrightarrow\left(x-2\right)^2+x-2=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow\left(x-2\right)\left(x-2+1\right)=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow x-2=-\sqrt{3x-2}\)
\(\Leftrightarrow2-x=\sqrt{3x-2}\)
\(\Leftrightarrow\left(2-x\right)^2=\left(\sqrt{3x-2}\right)^2\)
\(\Leftrightarrow4-4x+x^2=3x-2\)
\(\Leftrightarrow x^2-7x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\) (vi-et )
Vậy S=\(\left(1;6\right)\)
 Giúp e với ạaaaaa
Giúp e với ạaaaaa
Em cần giúp điều gì em nhỉ?
Ét o ét giúp mik với ạaaaaa
13C
14C
15C
16B
17A
18C
19A
20B
trong pascal, nêu lệnh điều kiện được sử dụng khi nào, nêu cấu trúc của câu lệnh điều kiện dạng đầy đủ và cách thực hiện câu lệnh
giúp mình với ạaaaaa