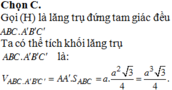Tính \(x_{ΔSABC}\) biết SABC là h/c đều có tất cả các cạnh = a
SH
Những câu hỏi liên quan
Tính thể tích SABC biết SABC là h/c đều có tất cả các cạnh = a
Tính VSABCD�Δ���� biết SABCD là h/c đều có tất cả các cạnh a
Đọc tiếp
Tính biết SABCD là h/c đều có tất cả các cạnh = a
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ACBD\right)\)
\(AC=AB\sqrt{2}=a\sqrt{2}\Rightarrow AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
Pitago tam giác vuông SAO:
\(SO=\sqrt{SA^2-AO^2}=\sqrt{a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{2}}{2}.a^2=\dfrac{a^3\sqrt{2}}{6}\)
Đúng 1
Bình luận (0)
Tính thể tích SABCD biết SABCD là h/c đều có tất cả các cạnh = a
Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a. Tính thể tích của (H). A.
a
3
2
B.
a
3
3
2
C.
a
3...
Đọc tiếp
Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a. Tính thể tích của (H).
A. a 3 2
B. a 3 3 2
C. a 3 3 4
D. a 3 2 3
Chọn C.
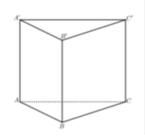
Gọi (H) là lăng trụ đứng tam giác đều ABC.A'B'C'
Ta có thể tích khối lăng trụ ABC.A'B'C' là:
V = A A ' . S A B C = a . a 2 3 4 = a 3 3 4
Đúng 0
Bình luận (0)
Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a. Tính thể tích của (H). A.
a
3
2
B.
a
3
3
2
C.
a
3
3...
Đọc tiếp
Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a. Tính thể tích của (H).
A. a 3 2
B. a 3 3 2
C. a 3 3 4
D. a 3 2 3
Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích của (H). A.
a
3
3
2
B.
a
3
3
4
C.
a
3
3
D.
a...
Đọc tiếp
Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích của (H).
A. a 3 3 2
B. a 3 3 4
C. a 3 3
D. a 3 2 6
Đáp án D
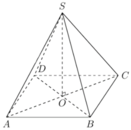
Gọi khối chóp tứ giác đều đó là S. ABCD.
Gọi O là giao điểm hai đường chéo hình vuông ABCD, ta có SO là đường cao hình chóp.
S O = S A 2 - A O 2 = a 2 - a 2 2 2 = a 2 2
S A B C D = a 2
Vậy thể tích cần tìm là:
V = 1 3 . S A B C D . S O = 1 3 a 2 . a 2 2 = a 3 2 6
Đúng 0
Bình luận (0)
Cho hình chóp đều SABC tất cả các cạnh bằng a.Xác định góc giữa cạnh bên và mặt phẳng đáy
(Tự vẽ hình)
Do hình chóp \(S.ABC\) là hình chóp đều
\(\Rightarrow ABC\) là tam giác đều cạnh \(a\) và \(SO\perp\left(ABC\right)\) với \(O\) là tâm ngoại tiếp tam giác \(ABC\)
Gọi \(AH\perp BC\) thì \(H\) là trung điểm \(BC\)
Ta có: \(AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow AO=\dfrac{2}{3}AH=\dfrac{a\sqrt{3}}{3}\); \(OH=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\)
Ta có: \(\left(SA;\left(ABC\right)\right)=\left(SA,AO\right)=\widehat{SAO}\)
Tam giác \(SAO\) vuông tại \(O\Rightarrow cos\widehat{SAO}=\dfrac{AO}{SA}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SAO}\approx55^0\)
Lại có: \(\Delta SBC\) đều \(\Rightarrow SH=\dfrac{a\sqrt{3}}{2}\)
Ta có: \(\left(\left(SBC\right),\left(ABC\right)\right)=\widehat{SHO}\)
\(cos\widehat{SHO}=\dfrac{OH}{SH}=\dfrac{1}{3}\Rightarrow\widehat{SHO}\approx70,5^0\)
Đúng 0
Bình luận (0)
Lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng a. Tính khoảng cách h từ C đến (ABC). A. h
a
3
4
B. h
a
3
C. h
a
3
7
D. h
a
2
4
Đọc tiếp
Lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng cách h từ C' đến (A'B'C').
A. h = a 3 4
B. h = a 3
C. h = a 3 7
D. h = a 2 4
Hình chóp SABC có
∆
SAB và
∆
SBC là các tam giác đều cạnh a;
∆
SAC là tam giác vuông. Tính thể tích V của hình chóp SABC A. V
a
3
6
B. V
a
3
3
12
C. V
a
3
2...
Đọc tiếp
Hình chóp SABC có ∆ SAB và ∆ SBC là các tam giác đều cạnh a; ∆ SAC là tam giác vuông. Tính thể tích V của hình chóp SABC
A. V = a 3 6
B. V = a 3 3 12
C. V = a 3 2 12
D. V = a 3 6 24