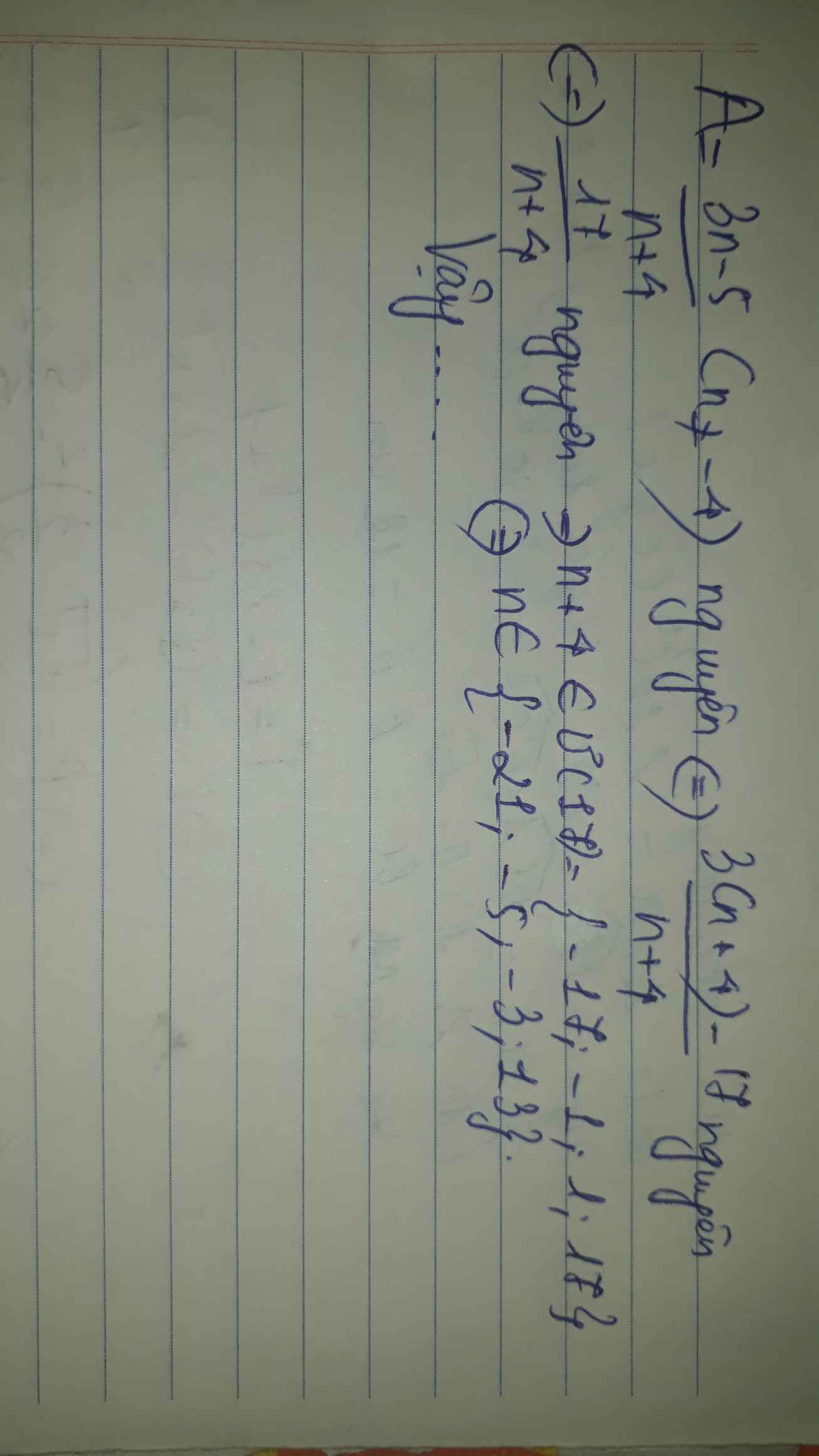cho A=3n-5:n+4. Tìm nϵZ để A có giá trị nguyên
HT
Những câu hỏi liên quan
Cho ps:
A=\(\frac{n+1}{n-3}\)(nϵZ;n#3)
a,Tìm a để có giá trị nguyên
b,Tìm a để có giá trị phân số
a) Để A có giá trị nguyên thì n + 1 chia hết cho n - 3
=> n - 3 + 4 chia hết cho n - 3
Mà n - 3 chia hết cho n - 3
=> 4 chia hết cho n - 3
=> n - 3 thuộc Ư(4)
=> n - 3 thuộc {-4; -2; -1; 1; 2; 4}
=> n thuộc {-1; 1; 2; 4; 5; 7}
b) Để A có giá trị phân số thì n - 3 khác 0
=> n khác 3
Đúng 0
Bình luận (0)
cho phân số a = n+1/n-3 (nϵz; n≠ 3)
a) Tìm n để A có giá trị nguyên
b) tìm n để A là phân số tối giản
Có thiệt là lớp 6 không vậy trời
Đúng 0
Bình luận (0)
tìm nϵZ để phân số n+5/n+3 có giá trị nguyên
Để phân số \(\dfrac{n+5}{n+3}\) có giá trị là số nguyên thì:
\(n+5⋮n+3\)
\(\Rightarrow n+3+2⋮n+3\)
\(\Rightarrow2⋮n+3\)
Vì \(n\in N\Rightarrow n+3\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Ta có bảng sau:
| n+3 | 1 | -1 | 2 | -2 |
| n | -2 | -4 | -1 | -5 |
Mà \(n\in N\) =>Không có giá trị của n để phân số đã cho nhận giá trị nguyên.
Đúng 2
Bình luận (1)
Xin lỗi mình nhìn lộn điều kiện của n.
Bạn chỉ cần làm giống bài mình ở dưới và cho thỏa mãn hết giá trị của n nhé. Nãy mình nhìn ra n là số tự nhiên nên loại hết đấy, vì đề là n thuộc tập sống nguyên nên chọn hết nhé bạn.
Đúng 2
Bình luận (2)
Để \(\dfrac{n+5}{n+3}\) là số nguyên thì:
n + 5 \(⋮\) n + 3
n + 3 + 2 \(⋮\) n + 3
\(\Rightarrow\left[{}\begin{matrix}n+3⋮n+3\\2⋮n+3\end{matrix}\right.\)
2 \(⋮\) n + 3
n + 3 \(\in\) Ư (2) = {-2 ; -1 ; 1 ; 2}
Lập bảng
| n + 3 | -2 | -1 | 1 | 2 |
| n | -5 | -4 | -2 | -1 |
\(\Rightarrow\)\(n\in\) {-5 ; -4 -2 ;-1}
Đúng 0
Bình luận (0)
Cho A=3n-5/n+4 . Tìm n là số nguyên để A có giá trị nguyên
Để \(A\) có giá trị nguyên thì \(\left(3n-5\right)⋮\left(n+4\right)\)
Ta có :
\(3n-5=3n+12-17=3\left(n+4\right)-17\) chia hết cho \(n+4\)\(\Rightarrow\)\(\left(-17\right)⋮\left(n+4\right)\)\(\Rightarrow\)\(\left(n+4\right)\inƯ\left(-17\right)\)
Mà \(Ư\left(-17\right)=\left\{1;-1;17;-17\right\}\)
Suy ra :
| \(n+4\) | \(1\) | \(-1\) | \(17\) | \(-17\) |
| \(n\) | \(-3\) | \(-5\) | \(13\) | \(-21\) |
Vậy \(n\in\left\{-3;-5;13;-21\right\}\)
Đúng 2
Bình luận (0)
A= 3n-5/n+4 = 3(n+4)-17/n+4 (n ≠ -4)
Để A ∈ Z ⇔ 17 chia hết cho n+4 hay n+4 ∈ Ư(17)
⇒ n+4 ∈ {17; -17; 1; -1}
n ∈ {13; -21; -3; -5}
Vậy n ∈ {13; −21; −3; −5}
Đúng 0
Bình luận (0)
Cho A=\(\dfrac{3n-5}{n+4}\) tìm n ϵ Z để A có giá trị nguyên
Cho A = 3n - 5/n + 4 . Tìm n thuộc Z để A có giá trị nguyên
ta có
\(A=\frac{3n-5}{n+4}=3-\frac{17}{n+4}\) là số nguyên khi \(\frac{17}{n+4}\text{ nguyên hay }n+4\text{ là ước của 17 }\)
\(\Rightarrow n+4\in\left\{\pm1,\pm17\right\}\Rightarrow n\in\left\{-21,-5,-3,13\right\}\)
Trả lời:
Ta có : A = \(\frac{3n-5}{n+4}=\frac{3\left(n+4\right)-17}{n+4}=\frac{3\left(n+4\right)}{n+4}-\frac{17}{n+4}=3+\frac{17}{n+4}\)
Để A = \(\frac{3n-5}{n+4}\)là số nguyên thì \(\frac{17}{n+4}\)cũng là số nguyên
=> \(17⋮n+4\)hay \(n+4\inƯ\left(17\right)=\left\{\pm1;\pm17\right\}\)
Ta có bảng sau:
| n+4 | 1 | -1 | 17 | -17 |
| n | -3 | -5 | 13 | -21 |
Vậy \(x\in\left\{-3;-5;13;-21\right\}\)thì A = \(\frac{3n-5}{n+4}\)là số nguyên.
Cho A= 3n-5/n+4. Tìm n để A có giá trị là một số nguyên
Cho A= 3n-5/n+4. tìm n thuộc Z để A có giá trị nguyên
để \(A\in Z\Rightarrow3n-5⋮n+4\left(n\in Z;n\ne-4\right)\left(1\right)\)
ta có \(n+4⋮n+4\)
\(\Rightarrow3\left(n+4\right)⋮n+4\)
\(\Rightarrow3n+12⋮n+4\left(2\right)\)
từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow3n+12-\left(3n-5\right)⋮n+4\)
\(\Rightarrow3n+12-3n+5⋮n+4\)
\(\Rightarrow17⋮n+4\)
\(\Rightarrow n+4\in\text{Ư}_{\left(17\right)}=\text{ }\left\{1;-1;17;-17\right\}\)
lập bảng giá trị
| \(n+4\) | \(1\) | \(-1\) | \(17\) | \(-17\) |
| \(n\) | \(-3\) | \(-5\) | \(13\) | \(-21\) |
vậy................
Đúng 0
Bình luận (0)
Để A có giá trị nguyên thì 3n - 5 \(⋮\)n + 4.
Ta có : 3n - 5 = 3(n + 4) - 17
Do n + 4 \(⋮\)n + 4
Để 3(n + 4) - 17 \(⋮\)n + 4 thì 17 \(⋮\)n + 4 => n + 4 \(\in\)Ư(17) = {1, -1, 17, -17}
Với : n + 4 = 1 => n = -3
n + 4 = -1 => n = -5
n + 4 = 17 => n = 13
n + 4 = -17 => n = -21
Vậy n = {-3; -5; 13; -21} thì A có giá trị nguyên.
Đúng 0
Bình luận (0)
Cho A= (3n-5)/(n+4)
Tìm n thuộc Z để A có giá trị nguyên
\(\frac{3n-5}{n+4}=\frac{3.\left(n+4\right)-17}{n+4}=\frac{3.\left(n+4\right)}{n+4}-\frac{17}{n+4}=3-\frac{17}{n+4}\)
Để \(3-\frac{7}{n+4}\) là số nguyên <=> \(\frac{17}{n+4}\)
=> n + 4 ∈ Ư ( 17 ) => Ư ( 17 ) = { ± 1 ; ± 17 }
=> n ∈ { - 5 ; - 3 ; - 21 ; 13 }
Đúng 0
Bình luận (0)
để A có giá trị nguyên thì 3n-5 chia hết cho n+4 ( điều kiện: n khác -4)
ta có 3n - 5 = 3(n+4) -17
vì 3(n+4) chia hết cho n+4 nên để 3(n+4) - 17 chia hết cho n+4 thì 17 chia hết cho n+4
=> n+4 là ước của 17
ta có ư(17) = -1;-17;1;17
nếu n+4=-1 thì n=-5 (thoả mãn)
nếu n+4 = -17 thì n=-21(thoả mãn)
nếu n+4 = 1 thì n= -3(thoả mãn)
nếu n+4 = 17 thì n= 16(thoả mãn)
Đúng 0
Bình luận (0)