chứng minh S=abc/R ( S là diện tích tam giác ABC ;R là tâm dường tròn ngoại tiếp tam giác )
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TQ
Những câu hỏi liên quan
Cho tam giác ABC có các cạnh BC = a, CA = b, AB = c. Gọi r là bán kính đường tròn nội tiếp, S là diện tích tam giác ABC.
a) Chứng minh : \(S=\dfrac{r\left(a+b+c\right)}{2}\)
b) Tính bán kính đường tròn nội tiếp của tam giác ABC. Biết tam giác ABC là tam giác cân có cạnh đáy bằng 16 cm, cạnh bên bằng 10 cm.
Hình như câu b chưa rõ lắm, tam giác ABC cân tại đâu?
Đúng 1
Bình luận (1)
Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).
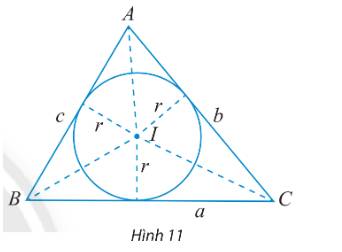
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.Chứng minh rằng
S
S
D
K
A
H
Đọc tiếp
Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.
Chứng minh rằng S ' S = D K A H
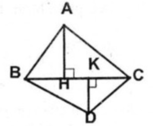
Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn tâm O, đường cao AH. Kẻ đường kính AD.
a) Chứng minh rằng: AB.AC=AH.AD
b) Gọi S là diện tích của tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. AB= c, AC=b, BC=a. Chưngs minh rằng: S=
abc/4R
chứng minh rằng tam giác ABC có chu vi 2p ngoại tiếp đường tròn (I ,r )thì diện tích S cửa tam giác có công thức S=p.r
Gọi O là tâm đường tròn nội tiếp tam giác ABC .Nối OA, OB, OC
Nối OA, OB, OC.Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBC.
Ta có:
Mà AB + AC + BC = 2p
Nên
Đúng 1
Bình luận (1)
Gọi I,E,F lần lược là tiếp điểm của đường tròn tâm O nội tiếp với AB,BC,CA
Ta có OI = OE = OF = r
S ABC = S AOB + S BOC + S COA = AB.OI/2 + BC.OE/2 + CA.OF/2 = (AB + BC + CA).r/2 = pr
Đúng 0
Bình luận (0)
Bài 2: Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O; R ). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H.Gọi S là diện tích tam giác ABC. a) Chứng minh các tử giác AEHF và AEDB nội tiếp được. b) Chứng minh AB. BC. AC=4RS c) Chứng minh OC vuông góc với DE và ( DE+EF+FD). R = 2S
a) Xét tứ giác AEHF có
\(\widehat{HEA}+\widehat{HFA}=180^0\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho tam giỏc ABC cú ba góc nhọn, nội tiếp đường tròn tâm O, bán kính R. Kẻ các đường cao AA’, BB’, CC’. Gọi S là diện tớch của tam giỏc ABC và S’ là diện tích của tam giác A’B’C’. 1) Chứng minh rằng AO vuông góc với B’C’
Giải chi tiết:
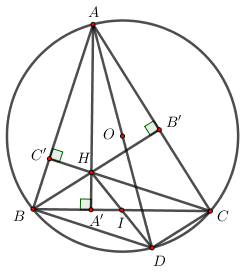
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
Xét tứ giác AB’HC’ có ∠AB′H+∠AC′H=900+900=1800⇒∠AB′H+∠AC′H=900+900=1800⇒ Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
Ta có ∠ABD=900∠ABD=900 (góc nội tiếp chắn nửa đường tròn) ⇒AB⊥BD⇒AB⊥BD.
Mà CH⊥AB(gt)⇒BD∥CHCH⊥AB(gt)⇒BD∥CH
Chứng minh tương tự ta có CD∥BHCD∥BH.
⇒⇒ Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)
Mà BC∩HD=I(gt)⇒IBC∩HD=I(gt)⇒I là trung điểm của BC.
c) Tính AHAA′+BHBB′+CHCC′AHAA′+BHBB′+CHCC′.
Ta có:
SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′
Chứng minh tương tự ta có: BHBB′=1−SHACSABC;CHCC′=1−SHABSABCBHBB′=1−SHACSABC;CHCC′=1−SHABSABC
⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2
Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức : S = p.r
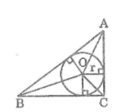
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : S A B C = S O A B + S O A C + S O B C
= (1/2).AB.r + (1/2).AC.r + (1/2).BC.r
= (1/2)(AB + AC + BC).r
Mà AB + AC + BC = 2p
Nên S A B C = (1/2).2p.r = p.r
Đúng 0
Bình luận (0)
Cho tam giác ABC có diện tích S. Gọi S1 là diện tích hình tròn ngoại tiếp tam giác, S2 là diện tích hình tròn nội tiếp tam giác. Chứng minh rằng 2S < S1 + S2.
Cho hình vuông biết diện tích là 81cm vuông.Tính độ dài một cạnh.
Chời ơi bài này dễ thế mà đứa học sinh lớp 1 còn biết làm?
EM MÌNH LỚP 1 NHẮM MẮT CŨNG LÀM ĐƯỢC NỮA



