tìm x,biết : x2-3x-4=0
tìm giá trị của ẩn số thỏa điều kiện cho sẵn
TM
Những câu hỏi liên quan
cho phương tình x2+x-m-2 (ẩn x)
a) tìm các giá trị của m để phương trình có nghiệm
b) tính giá trị của m, khi biết phương trình đã cho có hai nghiệm phân biệt x1,x2 thỏa mãn điều kiện x12 - x1x2 -2x2 = 16
\(\Delta=1-4\left(-m-2\right)\ge0\Leftrightarrow m\ge-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=-m-2\end{matrix}\right.\)
\(x_1^2-x_1x_2-2x_2=16\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)-2x_1x_2-2x_2=16\)
\(\Leftrightarrow-x_1-2\left(-m-2\right)-2x_2=16\)
\(\Leftrightarrow x_1+2x_2=2m-12\)
\(\Rightarrow x_1+x_2+x_2=2m-12\)
\(\Leftrightarrow-1+x_2=2m-12\Rightarrow x_2=2m-11\Rightarrow x_1=-1-x_2=-2m+10\)
Lại có: \(x_1x_2=-m-2\)
\(\Rightarrow\left(-2m+10\right)\left(2m-11\right)=-m-2\)
\(\Leftrightarrow4m^2-43m+108=0\Rightarrow\left[{}\begin{matrix}m=4\\m=\dfrac{27}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho x,y là hai số thực thỏa mãn điều kiện
x
2
+
y
2
+
x
y
+
4
4
y
+
3
x
. Tìm giá trị lớn nhất của biểu thức
P
3
(
x...
Đọc tiếp
Cho x,y là hai số thực thỏa mãn điều kiện x 2 + y 2 + x y + 4 = 4 y + 3 x . Tìm giá trị lớn nhất của biểu thức P = 3 ( x 3 - y 3 ) + 20 x 2 + 2 x y + 5 y 2 + 39 x .
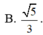
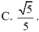
Cho phương trình bậc hai, ẩn số là x : x2 – 3x + k – 1 = 0.
Tìm giá trị của k sao cho phương trình đã cho có hai nghiệm x1, x2 thoả mãn điều kiện
x12 – x22 = 15.
\(\Delta=9-4\left(k-1\right)=13-4k\ge0\Rightarrow k\le\dfrac{13}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=k-1\end{matrix}\right.\)
\(\left(x_1-x_2\right)\left(x_1+x_2\right)=15\Leftrightarrow x_1-x_2=5\)
Kết hợp hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1-x_2=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=-1\end{matrix}\right.\)
\(x_1x_2=k-1\Rightarrow k-1=-4\Rightarrow k=-3\)
Đúng 1
Bình luận (2)
Cho
x
,
y
∈
R
thỏa mãn điều kiện
2
y
≥
x
2
và
y
≤
-
2
x
3
+
3
x
Tìm giá trị lớn nhất của biểu thức
P
x
2
+
y
2
A. 5 B. 4 C. 3 D. 2
Đọc tiếp
Cho x , y ∈ R thỏa mãn điều kiện 2 y ≥ x 2 và y ≤ - 2 x 3 + 3 x Tìm giá trị lớn nhất của biểu thức P = x 2 + y 2
A. 5
B. 4
C. 3
D. 2
Từ giả thiết bài toán suy ra
y ≥ 0 x 2 2 ≤ - 2 x 2 + 3 x ⇔ y ≥ 0 5 x 2 - 6 x ≤ 0 ⇔ y ≥ 0 0 ≤ x ≤ 6 5
Ta có
x 2 + y 2 ≤ x 2 + - 2 x 2 + 3 x 2 = 4 x 4 - 12 x 3 + 10 x 2
Ta có f ' x = 4 x x - 1 x - 5
f ' x = 0 x = 0 x = 1 x = 5 So điều kiện, chọn x = 0 ; x = 1 ; f(0); f(1) = 2; f 6 5 = 1224 625
Vậy m a x P = 2
Đáp án D
Đúng 0
Bình luận (0)
Cho các số thực x, y không âm và thỏa mãn điều kiện:
x
2
+
y
2
≤
2
. Hãy tìm giá trị lớn nhất của biểu thức:P
x
29
x
+
3
y...
Đọc tiếp
Cho các số thực x, y không âm và thỏa mãn điều kiện: x 2 + y 2 ≤ 2 . Hãy tìm giá trị lớn nhất của biểu thức:
P = x 29 x + 3 y + y 29 y + 3 x
Áp dụng bất đẳng thức Cosi ta có:
1 32 32 x 29 x + 3 y ≤ 1 4 2 32 x + 29 x + 3 y 2 = 1 8 2 61 x + 3 y
Tương tự
1 32 32 y 29 y + 3 x ≤ 1 8 2 61 y + 3 x
=> P ≤ 4 2 x + y ≤ 4 2 x 2 + 1 2 + y 2 + 1 2 = 8 2
Vậy P min = 8 2 <=> x = y = 1
Đúng 0
Bình luận (0)
Cho phương trình x^2_mx_2=0.tìm các giá trị của m để Pt có 2 nghiệm x1 và x2 thỏa mãn điều kiện x1x2+2x1+2x2=4
Phương trình là: \(x^2-mx-2=0\) đúng ko em nhỉ?
Đúng 0
Bình luận (1)
\(\Delta=m^2+8>0;\forall m\) nên pt đã cho luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-2\end{matrix}\right.\)
Ta có:
\(x_1x_2+2x_1+2x_2=4\)
\(\Leftrightarrow x_1x_2+2\left(x_1+x_2\right)=4\)
\(\Leftrightarrow-2+2m=4\)
\(\Leftrightarrow2m=6\)
\(\Leftrightarrow m=3\)
Đúng 1
Bình luận (0)
ND
29 tháng 10 2023 lúc 22:06
Cho các số thực x,y không âm thỏa mãn điều kiện x2+y2≤2�2+�2≤2.Hãy tìm giá trị lớn nhất của biểu thức P√x×(29x+3y)+√y×(29y+3x).
Đọc tiếp
Cho các số thực x,y không âm thỏa mãn điều kiện .Hãy tìm giá trị lớn nhất của biểu thức .
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2\leq (x+y)[(29x+3y)+(29y+3x)]=32(x+y)^2\leq 32.(x^2+y^2)(1+1)=64(x^2+y^2)\leq 64.2=128$
$\Rightarrow P\leq 8\sqrt{2}$
Vậy $P_{\max}=8\sqrt{2}$
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để pt x^2-(m-1)*x+4*m^2-m=0 có hai nghiệm trái dấu X1, X2 thỏa mãn điều kiện
2*(X1+X2)+3*x1*x2<2
a) Tìm các giá trị tham số m để phương trình x2 – (2m – 3)x + m(m – 3) 0 có 2 nghiêm phân biệt x1; x2 thỏa mãn điều kiện 2x1 – x2 4b) Cho Parabol (P): y-3x^2 và đường thẳng (d): y2x-m+9 .Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm nằm về hai phía của trục tung.
Đọc tiếp
a) Tìm các giá trị tham số m để phương trình x2 – (2m – 3)x + m(m – 3) = 0 có 2 nghiêm phân biệt x1; x2 thỏa mãn điều kiện 2x1 – x2 = 4
b) Cho Parabol (P): \(y=-3x^2\) và đường thẳng (d): \(y=2x-m+9\) .Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm nằm về hai phía của trục tung.