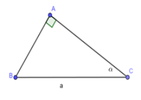
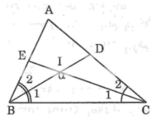
Cho tam giác ABC, góc A= α; phân giác trong của góc B và góc C gặp nhau ở M. phân giác ngoài của góc B và góc C gặp nhau ở N
a) Tính góc BMC và góc BNC theo α
b) c/m B,M,C,N thuộc đường tròn tâm O. Tìm vị trí của O
c) Tính số đo cung BMC và số đo cung BNC của (O)