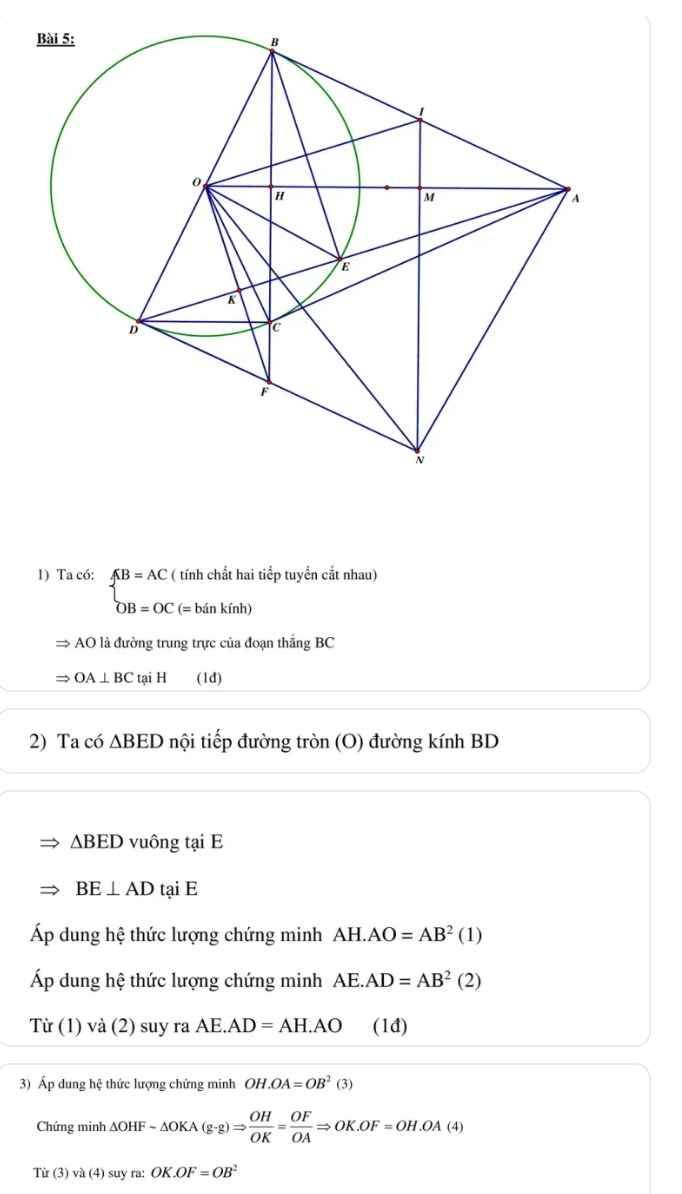
Cho A là một điểm nằm ngoài đường tròn \(\left(O;R\right)\). Qua A vẽ hai tiếp tuyến AB, AC \((\)B, C là tiếp điểm\()\). H là giao điểm của AO và BC. Kẻ đường kính BD; AD cắt \(\left(O\right)\) tại E.
a. Chứng minh: OA \(\perp\) BC và CD // OA.
b. Chứng minh: AH.AO \(=\) AE.AD và ∠AHE \(=\) ∠ADO.
c. Cho OB = 2cm, OA = 4 cm. Chứng minh: △ABC là tam giác đều và tính diện tích △ABC