So sánh s1 và s2
s1:2+4+6+...+5000
s2:2.2.5.5.5.5.2051
NT
Những câu hỏi liên quan
So sánh
S
1
và
S
2
S
1
−
2
+
−
4
+
−
6
+
(
−
8
)
+
...
+
−
50...
Đọc tiếp
So sánh S 1 và S 2
S 1 = − 2 + − 4 + − 6 + ( − 8 ) + ... + − 50 S 2 = − 1 + − 3 + − 5 + − 7 ... + − 49
So sánh : S1 = 1+2+2^2+2^3+...............+262014 và S2 = 2^2015-1
Cho các xâu
S1= ‘Pin_NLMT’
S2= ‘Pin_luthium’
S3= ‘Pin_JA_Solar’
S4= ‘Pin_Jinko_Solar’
a. So sánh các xâu sau: S1 và S4, S2 và S3
b. Thực hiện các thao tác: Insert(S1,S3,5)=?, Delete(S4,2,4)
Mọi người giúp mình với ạ!
uses crt;
const s1='Pin_NLMT'
s2='Pin_luthium'
s3='Pin_JA_Solar'
s4='Pin_Jinko_Solar'
begin
clrscr;
if s1<s4 then writeln('Xau s1 nho hon xau s4')
else if s1=s4 then writeln('Xau s1 bang xau s4)
else writeln('Xau s1 lon hon xau s4');
if s2<s3 then writeln('Xau s2 nho hon xau s3')
else if s2=s3 then writeln('Xau s2 bang xau s3')
else writeln('Xau s2 lon hon xau s3');
readln;
end.
Đúng 1
Bình luận (1)
Hãy so sánh hai quãng đường đi được s1 và s2.
cho S1=1+(-3)+5+(-7)...+17
cho S2=-2+4+(-6)+8+...+(-18)
tính S1 và S2
\(S_1=1+\left(-3\right)+5+\left(-7\right)+...+17\)
Số số hạng của tổng trên là: \(\frac{17-1}{2}+1=9\)
\(S_1=1+\left[-3+5\right]+\left[-7+9\right]+...+\left[-15+17\right]\)
\(S_1=1+2+2+2+2=9\)
\(S_2=-2+4+\left(-6\right)+8+...+\left(-18\right)\)
Số số hạng của tổng trên là: \(\frac{18-2}{2}+1=9\)
\(S_2=\left(-2+4\right)+\left(-6+8\right)+...+\left(-18\right)\)
\(S_2=2+2+2+2-18=-10\)
cho
s1: 1+ (-3) + 5 + (-7) + ... +17
s2 -2 + 4 + (-6) + 8 +... + (-18)
tính s1 và s2
kết bạn nha
s1 = 1+ (-3) +5 +(-7)+....+17 = (1+5+..+13+17)-(3+7+...+15)
Áp dụng công thức : tổng dãy số cách đều = số số hạng . tổng số đầu và số cuối chia đôi
s2 tương tự
Đúng 0
Bình luận (0)
cho S1 = 1 + (-3) + 5 + (-7) + ... + 17
S2 = -2 + 4 + (-6) + ...+ (-18)
tính tổng của S1 và S2
S1+S2=(1-2-3+4)+(5-6-7+8)+(9-10-11+12)+(13-14-15+16)+17-18
= 0 + 0 + 0 + 0 +17-18
=-1
Đúng 0
Bình luận (0)
Bài 4: Cho 2 điểm sáng S1 và S2 đặt trước gương a. Vẽ ảnh S1 S2 của S1 và S2 b. Xác định vùng đặt mắt để nhìn thấy ảnh S1 S2 c. Đặt mắt ở vị trí nào thì ảnh của điểm này che khuất ảnh của điểm kia giải nhanh giúp mình với
Đọc tiếp
Bài 4: Cho 2 điểm sáng S1 và S2 đặt trước gương a. Vẽ ảnh S1' S2' của S1 và S2 b. Xác định vùng đặt mắt để nhìn thấy ảnh S1' S2' c. Đặt mắt ở vị trí nào thì ảnh của điểm này che khuất ảnh của điểm kia giải nhanh giúp mình với
Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh 2a có diện tích xung quanh là
S
1
và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích là
S
2
. Khi đó, hệ thức giữa
S
1
và
S
2
là:A.
S...
Đọc tiếp
Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh 2a có diện tích xung quanh là S 1 và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích là S 2 . Khi đó, hệ thức giữa S 1 và S 2 là:
A. S 1 = S 2 B. S 1 = 4 S 2
C. S 2 = 2 S 1 D. 2 S 2 = 3 S 1
Chọn D.
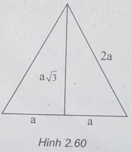
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
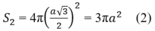
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1
Đúng 0
Bình luận (0)