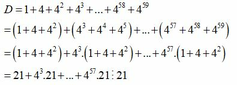Bài 1:

\(2^{49}=\left(2^7\right)^7=128^7;5^{21}=\left(5^3\right)^7=125^7\\ Vì:128^7>125^7\Rightarrow2^{49}>5^{21}\)

Bài 2:

\(a,S=1+3+3^2+3^3+...+3^{99}\\ =\left(1+3+3^2+3^3\right)+3^4.\left(1+3+3^2+3^3\right)+...+3^{96}.\left(1+3+3^2+3^3\right)\\ =40+3^4.40+...+3^{96}.40\\ =40.\left(1+3^4+...+3^{96}\right)⋮40\\ b,S=1+4+4^2+4^3+...+4^{62}\\ =\left(1+4+4^2\right)+4^3.\left(1+4+4^2\right)+...+4^{60}.\left(1+4+4^2\right)\\ =21+4^3.21+...+4^{60}.21\\ =21.\left(1+4^3+...+4^{60}\right)⋮21\)

Bài 1 :

\(2^{49}=\left(2^7\right)^7=128^7\)

\(5^{21}=\left(5^3\right)^7=125^7\)

mà \(125^7< 128^7\)

\(\Rightarrow2^{49}>5^{21}\)

Bài 2 :

a) \(S=1+3+3^2+3^3+...3^{99}\)

\(\Rightarrow S=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)...+3^{96}\left(1+3+3^2+3^3\right)\)

\(\Rightarrow S=40+40.3^4+...+40.3^{96}\)

\(\Rightarrow S=40\left(1+3^4+...+3^{96}\right)⋮40\)

\(\Rightarrow dpcm\)

b) \(S=1+4+4^2+4^3+...4^{62}\)

\(\Rightarrow S=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...4^{60}\left(1+4+4^2\right)\)

\(\Rightarrow S=21+4^3.21+...4^{60}.21\)

\(\Rightarrow S=21\left(1+4^3+...4^{60}\right)⋮21\)

\(\Rightarrow dpcm\)

\(C=1+3+3^2+3^3+\cdot\cdot\cdot+3^{11}\)

\(C=\left(1+3+3^2+3^3\right)+\left(3^4+3^5+3^6+3^7\right)+\left(3^8+3^9+3^{10}+3^{11}\right)\)

\(=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)+3^8\left(1+3+3^2+3^3\right)\)

\(=40+3^4\cdot40+3^8\cdot40\)

\(=40\cdot\left(1+3^4+3^8\right)\)

Vì \(40\cdot\left(1+3^4+3^8\right)⋮40\)

nên \(C⋮40\)

#\(Toru\)

\(C=1+3+3^2+3^3+...+3^{11}\)

\(\Rightarrow C=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)+3^8\left(1+3+3^2+3^3\right)\)

\(\Rightarrow C=40+3^4.40+3^8.40\)

\(\Rightarrow C=40\left(1+3^4+3^8\right)⋮40\)

\(\Rightarrow dpcm\)

A = 1 + 4 + 42 +43 +… + 458 +459

A = (l + 4 + 42) + (43 +44 + 45) + ... + (457+ 458 +459)

A = (1 + 4 + 42) + 43.(1 + 4 + 42) +... + 457 (1 + 4 + 42)

A= 21 + 43.21 + ... + 457.21 .

Do đó  A ⋮ 21

thế có chia hết cho 5 ko vậy

nhầm nhé so sorry

D = 1 + 4 + 4 2 + 4 3 + . . . + 4 58 + 4 59

=  1 + 4 + 4 2 +  4 3 + 4 4 + 4 5 + ... +  4 57 + 4 58 + 4 59

=  1 + 4 + 4 2 +  4 3 . 1 + 4 + 4 2 + ... +  4 57 . 1 + 4 + 4 2

=  21 + 21 . 4 3 + . . . + 21 . 4 57 ⋮ 21

A=(4+4^2)+...+4^22(4+4^2)

=20(1+...+4^22) chia hết cho 20

A=4(1+4+4^2)+...+4^22(1+4+4^2)

=21(4+...+4^22) chia hết cho 21

Vì A chia hết cho 20 và 21

và ƯCLN(20;21)=1

nên A chia hết cho 20*21=420

Lời giải:
$A=(4+4^2)+(4^3+4^4)+...+(4^{23}+4^{24})$

$=(4+4^2)+4^2(4+4^2)+...+4^{22}(4+4^2)$

$=(4+4^2)(1+4^2+....+4^{22})=20(1+4^2+...+4^{22})\vdots 20$

----------------------

$A=(4+4^2+4^3)+(4^4+4^5+4^6)+....+(4^{22}+4^{23}+4^{24})$

$=4(1+4+4^2)+4^4(1+4+4^2)+....+4^{22}(1+4+4^2)$

$=(1+4+4^2)(4+4^4+....+4^{22})=21(4+4^4+...+4^{22})\vdots 21$
--------------------------

Vậy $A\vdots 20; A\vdots 21$. Mà $(20,21)=1$ nên $A\vdots (20.21)$ hay $A\vdots 420$

viết dấu + cho nhanh, bạn!

A = 1 + 4 + 4² + 4³ + ... + 4²⁰²¹

A = 4⁰ + 4¹ + 4² + 4³ +...+ 4²⁰²¹

Xét dãy số 0; 1; 2; 3;...; 2021

Dãy số trên có số số hạng là:

(2021 - 0) : 1 + 1 = 2022

Vậy A có 2022 số hạng

vì 2022 : 3 = 674

Vậy ta nhóm 3 số hạng liên tiếp của A thành một nhóm thì khi đó

A = (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) +...+ (4²⁰¹⁹ + 4²⁰²⁰ + 4²⁰²¹)

A = (1 + 4 + 16) + 4³.(1 + 4 + 4²) + ... +4²⁰¹⁹.(1 + 4 + 4²)

A = 21 + 4³.21 +... + 4²⁰¹⁹.21

A = 21.(1 + 4³ + ... + 4²⁰¹⁹) 

21 ⋮ 21 ⇒ 21.(1 + 4³ + ...+ 4²⁰¹⁹) ⋮ 21 ⇒ A ⋮ 21 (đpcm)

Giải thích các bước giải:

A = 1 + 4 + 42 + 43 + ... + 42021

A = 40 + 41 + 42 + 43 +...+ 42021

Xét dãy số 0; 1; 2; 3;...; 2021

Dãy số trên có số số hạng là:

(2021 - 0) : 1 + 1 = 2022

Vậy A có 2022 số hạng

vì 2022 : 3 = 674

Vậy ta nhóm 3 số hạng liên tiếp của A thành một nhóm thì khi đó ta sẽ có

A = (1 + 4 + 42) + (43 + 44 + 45) +...+ (42019 + 42020 + 42021)

A = (1 + 4 + 16) + 43.(1 + 4 + 42) + ... +42019.(1 + 4 + 42)

A = 21 + 43.21 +... + 42019.21

A = 21.(1 + 43 + ... + 42019) 

21 ⋮ 21 ⇒ 21.(1 + 43 + ...+ 42019) ⋮ 21 ⇒ A ⋮ 21 (đpcm)

Vậy ta có thể biết A có thể chia hết cho 21 qua: 1+4+42+43+...+42021