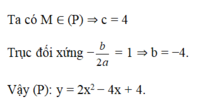Cho Parabal y= -x² + bx + c . Có điểm M(2;10) là điểm có tung độ lớn nhất. Tính giá trị của bc giải giúp e với chiều nay thi rồi ạaa
NH
Những câu hỏi liên quan
Cho parabal (P): y=-x^2 và đường thẳng (d) y= 2x+m. Xác định m để (P) cắt (d) tại 2 điểm pb có các hoành độ đề âm
Xét pt hoành độ giao điểm:
\(-x^2=2x+m\)
⇔ \(x^2+2x+m=0\) (1)
Để (P) cắt (d) tại 2 điểm phân biệt có hoành độ âm thì pt (1) có 2 nghiệm âm phân biệt. Do đó:
\(\left\{{}\begin{matrix}\Delta>0\\S< 0\\P>0\end{matrix}\right.\)⇔ \(\left\{{}\begin{matrix}4-4m>0\\-\dfrac{2}{1}< 0\left(TM\right)\\m>0\end{matrix}\right.\)⇔ \(\left\{{}\begin{matrix}m< 1\\m>0\end{matrix}\right.\)⇔ 0 < m < 1
Vậy để (P) cắt (d) tại 2 điểm phân biệt có hoành độ đều âm thì 0 < m < 1
Đúng 2
Bình luận (0)
cho parabal (P) y=x2 vad đtg (d) y=2mx-m2 +1 Tìm m để d cắt P tại 2 điểm phân biệt A,B có hoành độ x1, x2 mà \(\frac{1}{x1}+\frac{1}{x2}=\frac{3}{4}\)
Mn hộ mik vs ạ :)
Bài tập Cho hs y=-3x+b . Hãy xác định b nếu :
a, Đths cắt trục tung tại 3
b, Đths cắt đths y=6x+5 tại 1 điểm nằm nằm trên trục tung
c, Đths tiếp xúc parabal y=x^2
a, Vì đồ thị hàm số y= -3x + b cắt trục tung tại điểm có tung độ bằng 3
Nên y sẽ có giá trị bằng 3 và x có gá trị bằng 0
Thay y=3 ; x=0 vào hàm số ta đc: b=3
b, Vì Đths y= -3x + b cắt Đths y= 6x +5
Xét pt hoành độ giao điểm ta có: -3x + b = 6x +5
Mà 2 Đths cắt nau tại 1 điểm nằm trên truc tung nên x=0
Thay x=o vào pt trên ta đc b=5
c, Đths y=-3x+b giao vs parabal y=x^2
Xét pt hoành độ giao điểm ta có
x^2 = -3x + b => x^2 +3x -b = 0
Xét đen-ta của pt trên ta đc Đen-ta= b^2 - 4ac= 9+4b
mà Đths và parabal tiếp xúc nhau nên Đen-ta =0
Hay 9+4b=0 =>b=-9/4
Cho a,b,c∈R sao cho hàm số
yx
3
+
ax
2
+
bx
+
c
đạt cực trị tại x 2 đồng thời có y(0)1 và y(2)-3. Hỏi trong không gian Oxyz, điểm M(a;b;c) nằm trong mặt cầu nào sau đây? A.
(
x
-
1
)
2
+
(
y
-
1
)
2...
Đọc tiếp
Cho a,b,c∈R sao cho hàm số y=x 3 + ax 2 + bx + c đạt cực trị tại x = 2 đồng thời có y(0)=1 và y(2)=-3. Hỏi trong không gian Oxyz, điểm M(a;b;c) nằm trong mặt cầu nào sau đây?
A. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 16 .
B. ( x - 2 ) 2 + ( y - 3 ) 2 + ( z + 5 ) 2 = 64 .
C. x 2 + y 2 + ( z + 5 ) 2 = 36 .
D. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 .
Cho (P) y= x^2 + bx +c a) xác định P biết P nhận I(1;2) y= ax^2 +bx+c làm đỉnh. Xét sự biến thiên và vẽ đồ thị P b) xác định P biết P cắt trục tung tại điểm có tung độ=2 và nhận đồ thị x=-1 làm trục đối xứng
Xác định parabol (P): y 2
x
2
+ bx + c, biết rằng (P) đi qua điểm M(0;4) và có trục đối xứng x 1. A. y 2
x
2
− 4x + 4. B. y 2
x
2
+ 4x − 3. C. y 2
x
2
− 3x + 4. D. y 2
x
2
+ x + 4.
Đọc tiếp
Xác định parabol (P): y = 2 x 2 + bx + c, biết rằng (P) đi qua điểm M(0;4) và có trục đối xứng x = 1.
A. y = 2 x 2 − 4x + 4.
B. y = 2 x 2 + 4x − 3.
C. y = 2 x 2 − 3x + 4.
D. y = 2 x 2 + x + 4.
Parabol \(y=ax^2+bx+2\) đi qua điểm M ( 2 ; 3 ) và N ( -1 ; 4 ) có phương trình là :
A . \(y=x^2+x+2\)
B . \(y=\dfrac{5}{6}x^2-\dfrac{7}{6}x+2\)
C . \(y=2x^2-\dfrac{7}{2}x+2\)
D . \(y=x^2-x+2\)
Ta có:
Prabol đi qua điểm M(2;3) và N(-1,4)
=> \(\left\{{}\begin{matrix}4a+2b+2=3\\a-b+2=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}\\b=-\dfrac{7}{6}\end{matrix}\right.\)
=> chọn B
Đúng 2
Bình luận (0)
Cho hàm số y= x^3 + aX^2 + bx + c.
Tìm a,b,c để đồ thị hàm số đi qua điểm A(0;2) và đồ thị hàm số nhận điểm M(2;-2) là điểm cực tiểu
Cho (P) : y= x^2 + bx+ c. Tìm các số b,c để đồ thị là một parabol thỏa:
a) Đỉnh A(1;2)
b) Đỉnh I(-3;1)
c) Đi qua điểm M(1;-1) và có hoành độ đỉnh bằng 4.
d) Đi qua M(1;2) và có hoành độ đỉnh là 2.
e) Đi qua A(3;3) và có trục đối xứng là đường thẳng x = 1.