Cho tam giác ABC vuông tại A, trung tuyến AM. Kẻ MF vuông góc với AB( F thuộc AB ); ME vuông góc với AC ( E thuộc AC ) a, tứ giác AFME là hình gì ? vì sao? b, Kẻ AH vuông góc với BC ( H thuộc BC ); trên tia đối của tia HA lấy điểm D sao cho HD=HA; trên tia đối của tia HB lấy điểm K sao cho HK = HB. Chứng minh tứ giác ABDK là hình thoi
HN
Những câu hỏi liên quan
Cho tam giác ABC cân tại A. Kẻ đường trung tuyến BM .Từ M kẻ ME vuông góc với AB,MF vuông góc với AC(E thuộc AB,F thuộc AC).Chứng minh:
a)Tam giác BEM= tam giác CFM
b)AM là đường trung trực của EF
c)EF//BC
Sửa đề: Đường trung tuyến AM
a: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
góc B=góc C
=>ΔBEM=ΔCFM
b: ΔBEM=ΔCFM
=>BE=CF và ME=MF
AE+EB=AB
AF+FC=AC
mà EB=FC và AB=AC
nên AE=AF
mà ME=MF
nên AM là trung trực của EF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
Đúng 0
Bình luận (0)
a: ΔBEM=ΔCFM
b: AM là trung trực của EF
c: EF//BC
Đúng 0
Bình luận (0)
GIÚP MÌNH VỚI Ạ !!!!
Cho tam giác ABC vuông tại A, kẻ trung tuyến AM. Từ M kẻ ME vuông góc với AB, MF vuông góc với AC ( E thuộc AB, F thuộc AC)
a) Chứng minh tứ giác AEMF là hình chữ nhật.
b) Lấy điểm K đối xứng với điểm M qua F. Chứng minh AMCK là hình thoi.
c) Kẻ AH vuông góc với BC. Chứng minh tam giác EHF vuông.
Câu 10: Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc Với AC tại F.
a) Chứng minh ![]()
b) Chứng minh AM là trung trực của EF.
b) ta có tam giác ABC cân
=> \(\widehat{B}=\widehat{C}=180-\widehat{A}\) (1)
mà AM là trung tuyến => AM cx là phân giác và AM cx là đường cao (t/c tam giác cân)
=>\(\widehat{A1}=\widehat{A2}\)
xét tam giác AEM và tam giác AfM
có AM chung
\(\widehat{E}=\widehat{F}\)=90o
\(\widehat{A1}=\widehat{A2}\)
=> tam giác AEM =tam giác AFM (CH-GN)
=> AE =AC (2 cạnh tương ứng)
=> tam giác AEF cân ở \(\widehat{A}\)
=> \(\widehat{E}=\widehat{F}=180-\widehat{A}\) (2)
từ 1 và 2 =>\(\widehat{E}=\widehat{B}\) mà 2 góc ở vt đồng vị
=> EF // BC
mà AM ⊥ BC
=> EF ⊥ AM
=> AM là trung trực của EF (t/c tam giác cân)
Đúng 0
Bình luận (1)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC(M là trung điểm của BC)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng) và EB=FC(Hai cạnh tương ứng)
Ta có: AE+EB=AB(E nằm giữa A và B)
AF+FC=AC(F nằm giữa A và C)
mà EB=FC(cmt)
và AB=AC(ΔBAC cân tại A)
nên AE=AF
Ta có: AE=AF(cmt)
nên A nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ME=MF(cmt)
nên M nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của EF(Đpcm)
Đúng 0
Bình luận (0)
cho tam gvác abc vuông tại a trung tuyến am, đường cao ah .kẻ hd vuông góc với ab tại d ,he vuông góc ac tại e .a,chứng minh ah=de b,kẻ mf vuông góc vớv ab tại f lấy điểm k sao cho f là trung điểm của mk chứng minh tứ giác ambk la hinhf thoi và am vuông góc với de c, chứng minh bd.ac+ce.ab=ab.ac
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Từ M kẻ ME vuông góc với AB (E thuộc AB), MF vuông góc với AC (F thuộc AC)a) Tứ giác AEMF là hình gì? Vì sao?b) Cho biết AB 6 cm, AC 8 cm. Tính diện tích tứ giác AEMFc) Gọi N là điểm đối xứng với A qua M. Chứng minh: tứ giác ABNC là hình chữ nhậtd) Tam giác ABC có thêm điều kiện gì để tứ giác AEMF là hình vuông(Gải nhanh giúp mik với! Mk cần gấp! Cảm ơn)
Đọc tiếp
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Từ M kẻ ME vuông góc với AB (E thuộc AB), MF vuông góc với AC (F thuộc AC)
a) Tứ giác AEMF là hình gì? Vì sao?
b) Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tứ giác AEMF
c) Gọi N là điểm đối xứng với A qua M. Chứng minh: tứ giác ABNC là hình chữ nhật
d) Tam giác ABC có thêm điều kiện gì để tứ giác AEMF là hình vuông
(Gải nhanh giúp mik với! Mk cần gấp! Cảm ơn)
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
b: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
=>AE=3cm
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
=>AF=4cm
\(S_{AEMF}=AE\cdot AF=3\cdot4=12\left(cm^2\right)\)
c: Xét tứ giác ABNC có
M là trung điểm của BC
M là trung điểm của AN
Do đó: ABNC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABNC là hình chữ nhật
Đúng 0
Bình luận (1)
Cho tam giác ABc cân tại A đường trung tuyến AM ( M thuộc BC)
a, C/ m tam giác ABM =ACM
Từ M kẻ ME vuông góc AB tại E kẻ MF vuông góc vs AC tại F
C/m AM trung trực È
a) Xét ΔABM và ΔACM có:
AB = AC (ΔABC cân tại A)
Cạnh AM chung
BM = CM (AM là đường trung tuyến của BC)
⇒ ΔABM = ΔACM (c.c.c)
Vậy ΔABM = ΔACM
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A vẽ trung tuyến AM . Từ M kẻ ME vuông góc với AB tại E , kẻ MF vuông góc với AC tại F
a, chứng minh tam giác BEM = tam giác CFM
b, chứng minh AM là đường trung trực của EF
a./ \(\Delta BEM=\Delta CFM\)vì:
góc BEM = góc CFM ( = 90o )góc EBM = góc FCM (2 góc bằng nhau của tam giác cân ABC tại A)=> góc EMB = góc FMC ( = 180o - 2 góc bằng nhau)MB = MC (vì AM là trung tuyến).b./ => ME = MF (cạnh tương ứng của 2 tam giác bằng nhau) => M nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (1)
\(\Delta BEM=\Delta CFM\)=> BE = CF => AE = AF ( vì cùng bằng AB - BE = AC - CF)
=> A nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (2)
Từ (1) (2) => AM là trung trực của EF.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F a) Chứng minh: ∆BEM ∆CFM b) Chứng minh AM là trung trực của đoạn thẳng EF c) Chứng minh EF//BC d) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau ở D. Chứng minh ba điểm A, M, D thẳng hàng
Đọc tiếp
Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F a) Chứng minh: ∆BEM = ∆CFM b) Chứng minh AM là trung trực của đoạn thẳng EF c) Chứng minh EF//BC d) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau ở D. Chứng minh ba điểm A, M, D thẳng hàng
a: Xét ΔEBM vuông tại E và ΔFCM vuông tại F có
MB=MC
góc B=góc C
=>ΔEBM=ΔFCM
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>AE=AF
mà ME=MF
nên AM là trung trực của EF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
d: Xet ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
=>ΔABD=ΔACD
=>BD=CD
=>D nằm trên trung trực của BC
=>A,M,D thẳng hàng
Đúng 2
Bình luận (0)
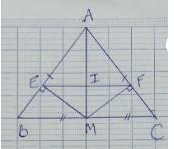
Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. a) Chứng minh ΔAMB ΔAMC b) Từ M vẽ ME vuông góc với AB (E AB) và MF vuông góc với AC (F AC). Chứng minh: ME MF c) So sánh ME với MC d) Kẻ BK là phân giác góc ABC (K AC); BK cắt AM tại I. Chứng minh CI là phân giác của góc ACB.
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM.
a) Chứng minh ΔAMB = ΔAMC
b) Từ M vẽ ME vuông góc với AB (E ![]() AB) và MF vuông góc với AC (F
AB) và MF vuông góc với AC (F ![]() AC). Chứng minh: ME = MF
AC). Chứng minh: ME = MF
c) So sánh ME với MC
d) Kẻ BK là phân giác góc ABC (K ![]() AC); BK cắt AM tại I. Chứng minh CI là phân giác của góc ACB.
AC); BK cắt AM tại I. Chứng minh CI là phân giác của góc ACB.
a) Xét AMB và AMC
ta có: AB=AC ( vì ABC cân tại A )
BM=MC ( vì AM là đường trung tuyến )
AM: cạnh chung
Suy ra: AMB = AMC ( c.c.c )
Đúng 0
Bình luận (0)






