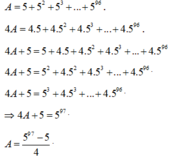Tính tổng A=5+52+53+...+52023
HP
Những câu hỏi liên quan
cho A=1+5+52+53+...+52023
so sánh 4.A với 52024
Ta có :
A = 1 + 5 + \(5^2\)+\(5^3\)+...+ \(5^{2023}\)
5A = 5 + \(5^2\)+\(5^3\)+\(5^4\)+..+ \(5^{2024}\)
=> 5A - A = ( 5 + \(5^2\)+\(5^3\)+\(5^4\)+..+ \(5^{2024}\) ) - ( 1 + 5 + \(5^2\)+\(5^3\)+...+ \(5^{2023}\) )
=> 4A = \(5^{2024}\)- 1
Nhận thấy :
\(5^{2024}\) - 1 > \(5^{2024}\)
=> 4A < \(5^{2024}\)
Vậy 4A < \(5^{2024}\)
Đúng 2
Bình luận (0)
1)Tìm số dư của phép chia B cho 4
B=1+3+32+33+...+3100
2)Thu gọn C=5-52+53-54+...+52023-52024
Bài 1:
$B=1+3+3^2+3^3+...+3^{100}$
$=1+(3+3^2)+(3^3+3^4)+...+(3^{99}+3^{100})$
$=1+3(1+3)+3^3(1+3)+...+3^{99}(1+3)$
$=1+(1+3)(3+3^3+...+3^{99})=1+4(3+3^3+....+3^{99})$
$\Rightarrow B$ chia 4 dư 1.
Đúng 1
Bình luận (0)
Bài 2:
$C=5-5^2+5^3-5^4+...+5^{2023}-5^{2024}$
$5C=5^2-5^3+5^4-5^5+...+5^{2024}-5^{2025}$
$\Rightarrow C+5C=5-5^{2025}$
$6C=5-5^{2025}$
$C=\frac{5-5^{2025}}{6}$
Đúng 2
Bình luận (0)
60-[ 36 + 43 ) : 52 ]
52023 : 5 2021 + 32 × 22 + 20240
\(=60-\dfrac{\left[36+64\right]}{25}\)
\(=60-4=56\)
Đúng 0
Bình luận (0)
\(60-[(36+4^3):5^2]\\=60-[(36+64):25]\\=60-(100:25)\\=60-4\\=56\)
Đúng 2
Bình luận (0)
60 -[ 36 + 4^3 ) :5^2
\(=60-(36+64)\div25\)
\(=60-100\div25\)
\(=60-4\)
=56
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tính tổng: A = 5 + 5 2 + 5 3 + ... + 5 96
Tính tổng sau:
A=2+22+23+...+219+220
B=5+52+53+...+550
C=1+3+32+33+...+3100
\(A=2+2^2+...+2^{20}\)
\(2A=2^2+2^3+...+2^{21}\)
\(2A-A=2^2+2^3+...+2^{21}-2-2^2-...-2^{20}\)
\(A=2^{21}-2\)
___________
\(B=5+5^2+...+5^{50}\)
\(5B=5^2+5^3+...+5^{51}\)
\(5B-B=5^2+5^3+...+5^{51}-5-5^2-...-5^{50}\)
\(4B=5^{51}-5\)
\(B=\dfrac{5^{51}-5}{4}\)
___________
\(C=1+3+3^2+...+3^{100}\)
\(3C=3+3^2+...+3^{101}\)
\(3C-C=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}\)
\(2C=3^{101}-1\)
\(C=\dfrac{3^{101}-1}{2}\)
Đúng 3
Bình luận (0)
2A= 2(2+22+23+...+219+220)
2A= 22+23+24+...+220+221
2A-A=(22+23+24+...+220+221)-(2+22+23+...+219+220)
A=221-2
Vậy A=221-2
Làm tương tự nhee
Đúng 0
Bình luận (0)
Tính tổng :
B = 1 - 2 + 3 - 4 + 5 - 6 + ..... + 51- 52 + 53
B= 1-2+3-4+5-6+.........+ 51-52+53
b= (1-2)+(2-3)+(5-6)+..........+ (51-52)+53
B= (-1)+(-1)+(-1)+.....+(-1)+53 ( có 26 số -1)
B= (-26)+ 53
B= 27
Đúng 0
Bình luận (0)
Viết các kết quả sau dưới dạng một lũy thừa:
a)134.132
b)716: 713
c)26.2
d) (52023: 52019). 52
nhanh mình tick ạ !!
a) 134 . 132 = 136
b) 716 : 713 = 73
c) 26 . 2 = 27
d) (52023 : 52019) . 52 = 54 . 52 = 56
Đúng 1
Bình luận (0)
a) \(13^4\cdot13^2=13^{4+2}=13^6\)
b) \(7^{16}:7^{13}=7^{16-13}=7^3\)
c) \(2^6\cdot2=2^{6+1}=2^7\)
d) \(\left(5^{2023}:5^{2019}\right)\cdot5^2\)
\(=5^{2023-2019}\cdot5^2\)
\(=5^2\cdot5^2\)
\(=5^{2+2}=5^4\)
Đúng 1
Bình luận (0)
a) Là bằng 136 á
b) Là bằng 73 á
c) Là bằng 27 á
d) Là bằng 56 á
Đúng 0
Bình luận (0)
Cho tổng A: 5+52+53+......+512
Chứng minh A chia hết cho (2.3.5)
\(A=5\left(1+5\right)+...+5^{11}\left(1+5\right)\)
\(=6\cdot\left(5+...+5^{11}\right)⋮30\)
Đúng 0
Bình luận (0)
Ta có: A 5 + 52 + 53 +....+ 5100
⇒A(5+52)+(53+54)+...+(599+5100)⇒A(5+52)+(53+54)+...+(599+5100)
⇒A5(1+5)+53.(1+5)+...+599.(1+5)⇒A5(1+5)+53.(1+5)+...+599.(1+5)
⇒A5.6+53.6+...+599.6⇒A5.6+53.6+...+599.6
A6.(5+53+...+599)A6.(5+53+...+599) chia hết
Ta có: A 5 + 52 + 53 +....+ 5100
⇒A(5+52)+(53+54)+...+(599+5100)⇒A(5+52)+(53+54)+...+(599+5100)
⇒A5(1+5)+53.(1+5)+...+599.(1+5)⇒A5(1+5)+53.(1+5)+...+599.(1+5)
⇒A5.6+53.6+...+599.6⇒A5.6+53.6+.....
Đọc tiếp
Ta có: A = 5 + 52 + 53 +....+ 5100
chia hết
Ta có: A = 5 + 52 + 53 +....+ 5100
Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip
Đúng 0
Bình luận (0)