giải phương trình với tham số a
4ax3-12x2-ax+3=0
TT
Những câu hỏi liên quan
Cho hàm số f x = 1 3 x 3 - 1 2 x 2 - 4 x + 6
Giải phương trình f"(cos x) = 0
Cho hàm số
f x = 1 3 x 3 - 1 2 x 2 - 4 x + 6
Giải phương trình f'(sin x) = 0.
Cho phương trình 1 2 x 2 - 2 x + 1 = 0
Giải phương trình đã cho bằng công thức nghiệm, so sánh với kết quả tìm được trong câu a.
Tìm các giá trị của tham số m để phương trình
1
2
x
2
−
4
x
+
3
m
2
có 3 nghiệm phân biệt A. m 3 B.
−
3
m
3
C.
m
±
3
D. Không tồn tại
Đọc tiếp
Tìm các giá trị của tham số m để phương trình 1 2 x 2 − 4 x + 3 = m 2 có 3 nghiệm phân biệt
A. m = 3
B. − 3 < m < 3
C. m = ± 3
D. Không tồn tại
Giải các phương trình trùng phương 1 3 x 4 - 1 2 x 2 + 1 6 = 0
Đặt m = x 2 .Điều kiện m ≥ 0
Ta có: 1/3. x 4 - 1/2. x 2 +1/6 =0⇔ 2 x 4 -3 x 2 +1=0 ⇔ 2 m 2 -3m + 1 =0
Phương trình 2 m 2 -3m + 1 =0 có hệ số a=2,b=-3,c=1 nên có dạng a +b+c =0
suy ra: m 1 = 1 , m 2 = 1/2
Ta có: x 2 = 1 ⇒ x = ± 1
x 2 = 1/2 ⇒ x = ± 2 /2
Vậy phương trình đã cho có 4 nghiệm :
x 1 =1 ; x 2 =-1 ; x 3 =( 2 )/2; x 4 = - 2 /2
Đúng 0
Bình luận (0)
Giải các phương trình: 3x4 – 12x2 + 9 = 0
Cả ba phương trình trên đều là phương trình trùng phương.
3x4 – 12x2 + 9 = 0 (1)
Đặt x2 = t, t ≥ 0.
(1) trở thành: 3t2 – 12t + 9 = 0 (2)
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1 và t2 = 3.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x2 = 3 ⇒ x = ±√3.
+ t = 1 ⇒ x2 = 1 ⇒ x = ±1.
Vậy phương trình có tập nghiệm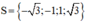 
Đúng 0
Bình luận (0)
(1) Cho phương trình bậc hai ẩn x ( m là tham số)x^2-4x+m=0(1) a) Giải phương trình với m =3 b) Tìm đk của m để phương trình (1) luôn có 2 nghiệm phân biệt (2) Cho phương trình bậc hai x^2-2x -3m+1=0 (m là tham số) (2) a) giải pt với m=0 b)Tìm m để pt (2) có nghiệm phân biệt. ( mng oii giúp mk vs mk đang cần gấp:
Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Đúng 1
Bình luận (0)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1
Đúng 1
Bình luận (0)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
7
x
2
−
2
x
+
3
0
b
)
5
x
2...
Đọc tiếp
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
7 x 2 − 2 x + 3 = 0 b ) 5 x 2 + 2 10 x + 2 = 0 c ) 1 2 x 2 + 7 x + 2 3 = 0 d ) 1 , 7 x 2 − 1 , 2 x − 2 , 1 = 0
a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai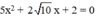 
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai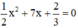 
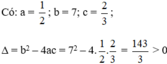
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt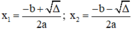 
+ Nếu Δ = 0, phương trình có nghiệm kép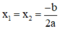 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Cho phương trình \(\left(x^2+ax+1\right)^2+a\left(x^2+ax+1\right)+1=0\) với a là tham số. Khi phương trình có nghiệm thực duy nhất, cmr a > 2
Sai đề.
Tại a=3 thay vào pt ban đầu \(\Rightarrow\left(x^2+3x+1\right)^2+3\left(x^2+3x+1\right)+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+3x+1=\dfrac{-3+\sqrt{5}}{2}\\x^2+3x+1=\dfrac{-3-\sqrt{5}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+3x+\dfrac{5-\sqrt{5}}{2}=0\left(1\right)\\x^2+3x+\dfrac{5+\sqrt{5}}{2}=0\left(2\right)\end{matrix}\right.\)
Bấm máy thấy pt (1) có hai nghiệm, pt (2) vô nghiệm => Tại a=3 thì pt ban đầu có 2 nghiệm (Trái với điều phải cm)
Đúng 2
Bình luận (0)