Giải hộ mình câu 6 với mình cảm ơn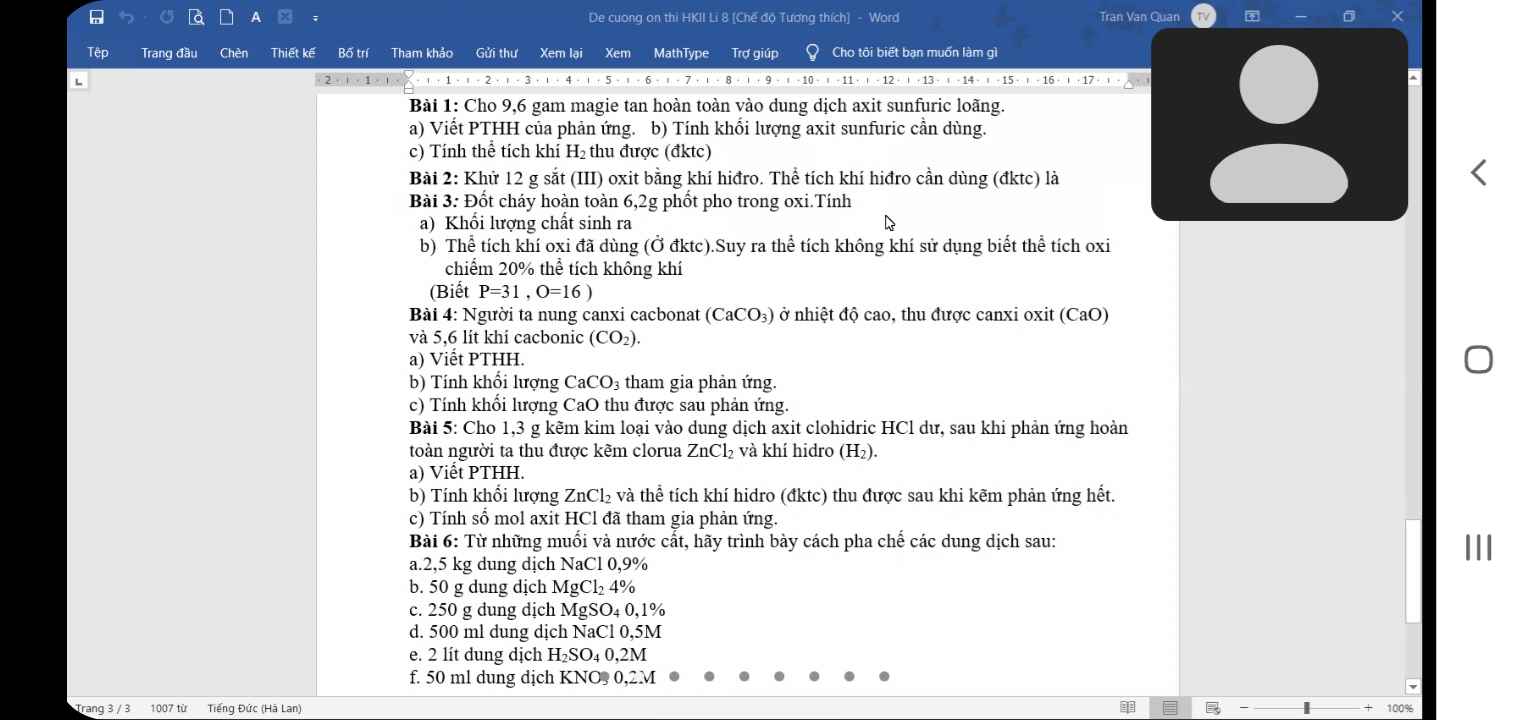
NM
Những câu hỏi liên quan
giải hộ mình câu 7,8,9 với ạ. Mình cảm ơn
Chữ mờ quá. Bạn nên gõ đề bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 1
Bình luận (0)
ai giải hộ mình câu 7,8,9 với mình cảm ơn
giải hộ mình câu 85,90 với ạ mình cảm ơn
giải hộ mình câu này với mình cảm ơn ạ
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp lắm ạ, làm nhanh hộ mình với <3
Cảm ơn lần nữa

1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
Đúng 0
Bình luận (0)
Hộ mình với. Giải giúp mình cả câu 3 với câu 4
Cảm ơn mọi người
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp, làm nhanh hộ mình với ạ <3

ext-9bosssssssssssssssss
Ai giải hộ mình câu này với....
6+1(5+3)
Cảm ơn nhiều!!!!
Dễ mà
6 + 1 + ( 5 + 3 )
7 + ( 5 + 3 )
7 + 8
= 15
Đúng 0
Bình luận (0)
6+1( 5+3)
= 7.8
= 56
bạn xem lại đề xem nha! Đề toán lớp 2 đây hả??
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải hộ mik câu này với mình cảm ơn.
Đọc tiếp
Giải hộ mik câu này với mình cảm ơn.
đk: \(\left\{{}\begin{matrix}x\ge-1\\y\ge-2\end{matrix}\right.\)
TheoBĐT Bunhiacopxki ,ta có: \(x-3\sqrt{x+1}=3\sqrt{y+2}-y\)
\(\Rightarrow\left(x+y\right)^2-9\left(\sqrt{x+1}+\sqrt{y+2}\right)^2\le9.2\left(x+y+3\right)\)
\(\Leftrightarrow\left(x+y\right)^2-18\left(x+y\right)-54\le0\)
\(\Rightarrow x+y\le9+3\sqrt{15}\Rightarrow P\le9+3\sqrt{15}\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+y=9+3\sqrt{15}\\\sqrt{x+1}=\sqrt{y+2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10+3\sqrt{15}}{2}\\y=\dfrac{8+3\sqrt{15}}{2}\end{matrix}\right.\)
Vậy Max P = \(9+3\sqrt{15}\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10+3\sqrt{15}}{2}\\y=\dfrac{8+3\sqrt{15}}{2}\end{matrix}\right.\)
===> Chọn D
Đúng 1
Bình luận (0)


