Chứng tỏ rằng
A= n/12+ n2/8 +n3/24 có giá trị nguyên với mọi n là số chẵn
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
chứng minh rằng với mọi n chẵn thì
\(\frac{n}{12}+\frac{n^2}{8}+\frac{n^3}{24}\) là số nguyên
\(\frac{n}{12}+\frac{n^2}{8}+\frac{n^3}{24}=\frac{2n+3n^2+n^3}{24}=\frac{n^3+2n^2+n^2+2n}{24}=\frac{n^2\left(n+2\right)+n\left(n+2\right)}{24}\)
\(=\frac{\left(n^2+n\right)\left(n+2\right)}{24}=\frac{n\left(n+1\right)\left(n+2\right)}{24}\)
Do n chẵn nên n=2k (k nguyên) => n+2=2k+2=2(k+1) => n(n+2)=2k.2(k+1)=4k(k+1)
k(k+1) là 2 số nguyên liên tiếp, trong đó có ít nhất 1 số chẵn nên k(k+1) chia hết cho 2 => 4k(k+1) chia hết cho 8
=>n(n+2) chia hết cho 8=>n(n+1)(n+2) chia hết cho 8 (1)
Mặt khác n;n+1;n+2 là 3 số nguyên liên tiếp nên trong đó có ít nhất 1 số chia hết cho 3 (tự chứng minh hoặc xem cách chứng minh trên mạng nhé)
=>n(n+1)(n+2) chia hết cho 3 (2)
Từ (1) và (2) và (3;8)=1 => n(n+1)(n+2) chia hết cho 3.8=24
=>\(\frac{n\left(n+1\right)\left(n+2\right)}{24}\) nguyên => đpcm
1. Cho A là tổng các số lẻ có 2 chữ số: 11+13+15+.....+99. Không tính giá trị của A, hãy cho biết A là số chẵn hay số lẻ.
2. Chứng tỏ rằng với mọi số tự nhiên n thì n mũ 2+n+1 không chia hết cho 5
3. Chứng tỏ rằng số a=9 mũ 11 +1 chia hết cho cả 2 và 5
4.Chứng tỏ rằng tích n(n+3) là số chẵn với mọi số tự nhiên
#ha le ha ban trả lời câu 2,3,4 giúp minh với
CMR: với n chẵn thì giá trị của biểu thức A = n^3/24 + n^3/8 + n/12 là một số nguyên
chứng tỏ rằng A= (n+9999)(n+2014) là một số chẵn với mọi số nguyên n
chứng minh rằng với n chẵn thì A= n/12 +n2/8 + n3/24 là số nguyên
A=a^3/24+a^2/8+a/12
= (a^3+ 3 a^2+ 2) /24 = a(a+1)(a+2)/24
ta cần CM a(a+1)(a+2) chia hết cho 24
để dễ hiểu mình sẽ trình bày cụ thể, còn nếu muốn rút gọn thì b có thể tự trình bày lại nhá :D
do a chắn => a=4k hoặc a=4k+2 (k thuộc Z)
TH1: a=4k; a+2=4k+2
=> a(a+1)(a+2) chia hết cho 4*2=8
và trong 3 số a, a+1, a+2 có 1 số chia hết cho 3 mà (3;8)=1
=> a(a+1)(a+2) chia hết cho 24
TH2: a=4k+2, a+2= 4k+4 (k thuộc Z)
=> a(a+1)(a+2) chia hết cho 4*2=8
và trong 3 số a, a+1, a+2 có 1 số chia hết cho 3 mà (3;8)=1
=> a(a+1)(a+2) chia hết cho 24
vậy A=a^3/24+a^2/8+a/12 luôn có giá trị nguyên
1) Đặt a=2k vì a chẵn
=>A = k^3/3+k^2/2+k/6 = (2k^3+3k^2+k)/6
= (2(k-1)k(k+1) + 3k(k+1))/6
=(k-1)k(k+1)/3 + k(k+1)/2
(k-1)k(k+1) là tích của ba số nguyên liên tiếp nên chia hết cho 3 =>(k-1)k(k+1)/3 nguyên
k(k+1) là tích của hai số nguyên liên tiếp nên chia hết cho 2 =>k(k+1)/2 nguyên
=>A nguyên
Chứng minh rằng với mọi số nguyên n thì (2 - n) ( n2 - 3n + 1) + n (n2 + 12 )+ 8 chia hết cho 5
\(\left(2-n\right)\left(n^2-3n+1\right)+n\left(n^2+12\right)+8\)
\(=2n^2-6n+2-n^3+3n^2-n+n^3+12n+8\)
\(=5n^2+5n+10\)
\(=5\left(n^2+n+2\right)⋮5\) (đpcm)
Chứng tỏ rằng với mọi giá trị n là số nguyên thì phân số (3n+10):(n+3) là phân số tối giản. Tìm giá trị nguyên n để phân số đó cs giá trị nguyên (héppp mii mình vộiii)
Gọi d=ƯCLN(3n+10;n+3)
=>3n+10-3n-9 chiahết cho d
=>1 chia hết cho d
=>d=1
=>PSTG
Chứng tỏ rằng với mọi x ≠ 0 và x ≠ ±a (a là một số nguyên), giá trị của biểu thức a - x 2 + a 2 x + a . 2 a x - 4 a x - a là một số chẵn.
Rút gọn biểu thức ta có:
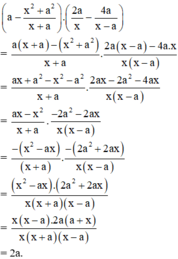
Với a là một số nguyên thì giá trị biểu thức bằng 2a là một số chẵn.
chứng tỏ rằng :với mọi số nguyên n thì (n+4).(n+7) luôn là một số chẵn
*Với n là số lẻ
=>n+4 là số lẽ;n+7 là số chẳn
=>(n+4)(n+7) là số chẳn
*Với n là số chẳn
=>n+4 là số chẳn;n+7 là số lẽ
=>(n+4)(n+7) là số chẳn
=>(n+4)(n+7) là số chẳn với mọi số nguyên n